5. ПЕРЕСТАНОВКИ ОБОЗНАЧЕНИЙ ДВУХ ФАЗ
Число перестановок обозначений двух фаз может быть равно трем по числу фаз, обозначения которых не изменяются, т. е. при перестановке двух фаз неизменным может оставаться обозначение либо фазы А, либо В, либо С на стороне ВН или соответственно на стороне НН для фаз а, b и с.
Перестановки могут быть одинарными — либо па стороне ВН, либо на стороне НН — и двойными, т. е. одновременно на сторонах ВН и НН. Двойные перестановки могут быть одноименными, когда переставляются обозначения двух одинаковых фаз, либо разноименными (при перестановке двух разных фаз на сторонах ВН и НН). В дальнейшем будет показано, что любая двойная разноименная перестановка двух фаз может быть представлена как результат двух преобразований: двойной одноименной перестановки и циклического перемещения на стороне ВН либо НН. Эти преобразования могут производиться и в обратном порядке: сначала циклическое перемещение на стороне ВН либо НН, а затем двойная перестановка.
Одинарные перестановки двух фаз дают такие схемы соединения, к которым не применимы часовые обозначения, так как векторы НН всех фаз имеют различный сдвиг фаз по отношению к векторам одноименных фаз ВН.
На рис. 15 показана схема соединения звезда/звезда, но на стороне НН средняя фаза сохраняет свое первоначальное обозначение b, тогда как обозначения крайних фаз на стороне ЙМ поменялись местами. 6 скобках показано исходное обозначение фаз, соответствующее схеме № 1 приложения 1. Совмещение центров обеих звезд показывает, что векторы фаз В и b совпадают «и им можно было бы дать обозначение 0 ч, но векторы фаз А и а имеют другой сдвиг фаз (8 ч), а фазы Си с имеют сдвиг на 4 ч.

Рис. 15. Одинарная перестановка двух фаз в схеме Y/Y-0 на стороне НН.
Это различие в сдвиге фаз объясняется тем, что после перестановки обозначений фаз на стороне НН получилось различное чередование векторов ВН и НН. Векторы А, В, С «вращаются» по часовой стрелке, а последовательность векторов а, b, с — против часовой стрелки.
На рис. 16 приведено построение векторной диаграммы для схемы треугольник/звезда при одинарной перестановке на стороне ВН. Исходное стандартное обозначение зажимов соответствует схеме № 5 приложения 1. Это исходное обозначение фаз ВН взято в скобки на рис. 16. Треугольник вершин А, В, С векторов междуфазных напряжений сети ВН остался без изменения, но перестановка фаз В я С сети привела к изменению чередования векторов в треугольнике на стороне ВН. Теперь горизонтально вправо направлен вектор ZC, тогда как в исходной схеме № 5 горизонтально влево был направлен вектор ХА.
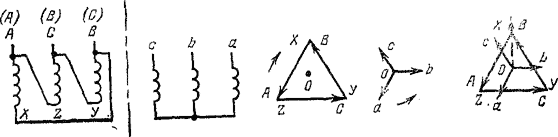
Рис. 16. Одинарная перестановка двух фаз на стороне ВН для схемы
Для векторов НН построение диаграммы обычное. Для обмотки на средней фазе вектор ob строим горизонтально вправо, так как на стороне ВН на этом сердечнике намотана обмотка ZC, вектор напряжения которой направлен горизонтально вправо. На левом стержне (со стороны отводов НН) находится фаза с. Для нее вектор ос строим параллельно вектору YB, так как на правом стержне со стороны отводов ВН находится фаза YB обмотки ВН.
Совмещение центров обеих векторных диаграмм показывает, что фазы В и b имеют группу 3, фазы А и а—11, а фазы С и- с — 7. Таким образом, здесь тоже получилась схема, для которой нельзя дать часового обозначения, ибо все векторы фаз НН имеют различный сдвиг фаз по сравнению с одноименными векторами фаз ВН.
Производя для любых схем из приложений 1 и 2 одинарные перестановки двух фаз, получаем, что эти перестановки дают всегда неприемлемые результаты — угол сдвига для одноименных фаз ВН и НН получаются различными и для таких схем часовые обозначения групп соединения применить нельзя.
Двойные одноименные перестановки двух фаз, т. е. перестановки двух одноименных фаз одновременно на сторонах НН и ВН как бы нейтрализуют искажения, вносимые каждой одинарной перестановкой двух фаз на сторонах ВН и НН порознь.
Двойные одноименные перестановки двух фаз обладают интересным свойством: они преобразуют группы в симметричные относительно оси 0—6 ч. Это означает, что группа 1 переходит в группу 11 и наоборот, группа 2 переходит в группу 10 и наоборот, группа 3 переходит в группу 9 и наоборот и т. д. Только группы 0 и 6 остаются неизменными при двойной одноименной перестановке.
В некоторых примерах применим все три одноименные перестановки двух фаз для одной и той же схемы. В этом случае верхняя строчка обозначений в кружках соответствует исходному обозначению в схемах из приложений 1 и 2. Следующая строчка без скобок соответствует случаю, когда обозначения фазы сети и трансформатора А а а остались без изменения, 'а обозначения двух других фаз взаимно изменились. Обозначения в квадратных скобках относятся к случаю, когда фазы В и b остались без изменения на своих местах, а в круглых скобках записаны обозначения при неизменном положении фаз С и с.
На рис. 17 показаны три двойные одноименные перестановки двух фаз для схемы № 18 из приложения 1. Эта схема имеет группу 11, л согласно сказанному выше эта группа должна после двойной одноименной перестановки .перейти в группу 1.
![]()
Рис. 17. Двойная одноименная перестановка для схемы
![]()
одноименной перестановке. Согласно ранее установленным условностям положение концов векторов А, В и С для фаз сети ВН в вершинах разностороннего треугольника не нарушается при изменении порядка присоединения этих фаз сети ВН к различным зажимам ВН трансформатора. На рис. 17 этим перестановкам соответствуют обозначения без скобок, в квадратных и круглых скобках. Но любая перестановка двух фаз на стороне ВН приводит к изменению фазных напряжений и направлений магнитных потоков в стержнях. До преобразования (обозначения в кружках) горизонтально вправо был направлен вектор ВН фазы С, .намотанной на правом стержне. После любой перестановки двух фаз горизонтально влево направлен вектор ВН фазы А. Это есть единственно возможное направление этого вектора ВН
На рис. 17 обозначения в кружках соответствуют исходной схеме A/Y, имеющей группу 11. Здесь построены для исходной группы треугольник векторов ВН и звезда векторов ИН. На рис. 17 показано также, как изменяются эти две векторные диаграммы при любой двойной
фазы, ибо после обхода обмотки фазы А, например намотанной на среднем стержне (для -преобразования в круглых скобках), должен произойти обход обмотки фазы В (в данном случае на левом стержне). После обхода фазы В на векторной диаграмме конец вектора напряжений фазы В должен оказаться в вершине В равностороннего треугольника векторов сети ВН. Таким образом, указанные выше положения вектора фазы А и вектора фазы В, непосредственно соединенной с обмоткой фазы А, независимо от нахождения этих обмоток па том или ином стержне оказываются единственно возможными для заданного треугольника векторов ВН сети и для любой перестановки обозначений фаз ВН.
Изменение направлений векторов ВН после любой перестановки фаз ВН приводит и к изменению направлений векторов НН. Однако при одновременной и одноименной перестановке фаз на сторонах ВН и ИИ для любой из этих перестановок сохраняется одноименность наименований обмоток ВН и НН на, одном каком-то стержне. Так, для преобразования, показанного в круглых скобках, фазы А я а оказались на среднем стержне, а фазы В и b — соответственно на левом и правом стержнях, т. е. фактически тоже на одном и том же стержне, ибо название левый или правый дается, когда смотрят со стороны отводов ВН для обмотки ВН или отводов НН для обмоток НИ.
Построение векторов НН фаз а, буквенные обозначения которых написаны без скобок, в квадратных скобках или в круглых скобках, а также векторов для напряжений фаз b я с особых трудов не представляет, и в результате этих построений легко убедиться, что теперь получилась схема Δ/Y-l вместо A/Y-11.
В качестве примера преобразования группы 1 в группу 11 на рис. 18 показаны все три возможные двойные одноименные перестановки двух фаз для схемы № 21 приложения 2. Для этого исходного положения на векторной диаграмме все обозначения заключены в кружки.
Перестановки двух фаз на стороне ВИ не вызовут никаких изменений исходной звезды векторной диаграммы на стороне ВН. Одноименные перестановки на стороне НН приведут также к тому, что при любой двойной перестановке одноименные наименования фаз на сторонах ВН и НН сохраняются. Это облегчает построение векторных диаграмм.
Звезда векторов для напряжений внутренних ветвей зигзага, идущих от нейтрали зигзага, примет ту же форму и положение, что для исходной схемы Y/Z-1. Только обозначения промежуточных зажимов будут различными для каждой одноименной перестановки.
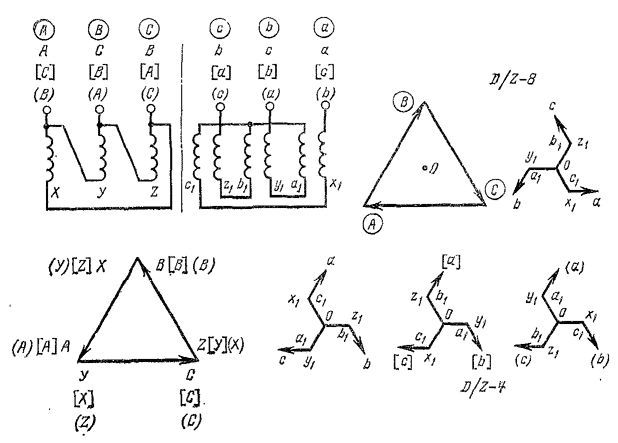
Рис. 18. Двойная одноименная перестановка для схемы
Y/Z-l—Y/Z-11.
Если, например, проследить за положением и обозначением промежуточных зажимов при разном положении фазы b, то легко увидеть, что в случае, когда положение фазы b осталось неизменным по сравнению с исходным (обозначения фаз в квадратных скобках), вектор obi занимает такое же положение, как и в исходной схеме Y/Z-1, Однако в этом случае фазы а и с (а также А и С) поменялись местами, и потому другие два вектора оа\ и ос\ тоже поменялись местами по сравнению с исходной схемой Y/Z-1.
Для преобразования при неизменном положении фазы b (обозначения в квадратных скобках) построение системы векторов НН ведем следующим образом. Промежуточный зажим b 1 соединен с другим промежуточным зажимом z\, от которого обход внешней ветви зигзага обмотки НИ происходит по обмотке на левом стержне. На нем намотана обмотка, соединенная с зажимом [11] на правом стержне со стороны отводов ВН.
Поэтому вектор НН этой внешней ветви от промежуточного зажима должен быть изображен вектором, параллельным вектору OA. Так строим вектор Z\ [а].
Вектор для внутренней ветви ось намотанной на том же левом стержне со стороны отводов НИ, должен, очевидно, иметь направление, обратное вектору О [А]. Промежуточный зажим Cj соединен непосредственно с зажимом Х\ на правом стержне со стороны НН, на котором, теперь уже левом стержне со стороны ВН, намотана обмотка ВН, соединенная с фазой [(С]. Поэтому вектор напряжения для внешней ветви зигзага от промежуточного зажима хх должен иметь направление, параллельное вектору О[С], и получить обозначение внешнего зажима [с], т. е. после междуфазного соединения С\Х\ строим вектор Х\ [с]. Наконец, .на этом же стержне находится внутренняя ветвь зигзага оаи по которой обход происходит в обратном направлении, чем по обмотке О [С] на стороне ВН. Поэтому для ветви зигзага ofli строим вектор оаи имеющий направление, обратное вектору 0[С]. Промежуточный зажим ах соединен непосредственно с зажимом у\ на среднем стержне. На нем со стороны ВН намотана обмотка, соединенная с фазой В сети. В силу этого от точки необходимо построить для внешней ветви зигзага вектор, параллельный и одинаково направленный с вектором 0{\В\. Так как зажим внешней ветви зигзага на среднем стержне имеет обозначение [ft], то, таким образом, строим вектор у1[b]. Совмещение центров тяжести диаграмм векторов ВН и НН показывает, что эта двойная одноименная перестановка дает группу 11.
Аналогичные построения для других одноименных двойных перестановок (когда сохраняют свое место фазы Л и а обозначения в круглых скобках) показывают, что эти перестановки то же дадут группу 11.
Соответствующие построения векторов НН диаграмм (с обозначениями без скобок и в круглых скобках) даны на рис. 18 со всеми обозначениями векторов для внутренних и внешних ветвей зигзага.
На рис. 19 и 20 показано преобразование четных групп в симметричные относительно оси 0—6 ч. Исходная схема № 28 приложения 2 показана на рис. 19 с обозначениями фаз, взятыми в кружки. Как и для схемы, показанной на рис. 17, здесь тоже любая перестановка двух фаз на стороне ВН приводит к изменению направ- лений векторов, образующих равносторонний треугольник, но положение и наименование вершин этого треугольника векторов ВН сети остаются неизменными. Переходя к построению векторной диаграммы на стороне НН, видим, что двойная одноименная перестановка фаз приводит в первую очередь к изменению направления и положения звезды векторов для внутренних ветвей

Рис. 19. Двойная одноименная перестановка для схемы A/Z-8—>AjZA.
зигзага. На самом деле, если взять преобразование, при котором сохраняют свое положение фазы (С) и (с), т. е. для обозначений в круглых скобках, то обход по внутренней ветви зигзага на среднем стержне должен дать вектор obi, параллельный и одинаково направленный с вектором Y(Л) обмотки ВН на том же среднем стержне. Промежуточный зажим b\ при помощи междуфазного отвода соединяется с промежуточным зажимом zu от которого обход будет производиться по обмотке, намотанной на левом со стороны отводов НН стержне. На том же стержне, правом со стороны отводов ВН, намотана обмотка ВН 2(C), соединенная с фазой С сети. Обход по обмоткам ВН и НИ на этом стержне происходит в одном направлении — снизу вверх, но так как эти
обмотки имеют разное направление намотки, то векторы для напряжения в этих обмотках должны иметь разное направление. Для фазы ВН вектор Z(C) направлен горизонтально вправо. Поэтому вектор Zi(c) должен быть направлен горизонтально влево и -иметь обозначения внешнего зажима (с).

Рис. 20. Двойная одноименная перестановка для схемы
Δ/Δ-10—"-Δ/Δ-2.
Очевидно, при обходе внутренней ветви обмотки НН на том же -стержне может быть построен вектор ось направленный обратно вектору Z\{c). Промежуточные зажимы С\ и Х[ соединены накоротко, и от Х\ обход производится по внешней ветви зигзага, намотанной на правом со стороны НН стержне. На том же стержне, левом со стороны отводов ВН, намотана обмотка ВН, соединенная с фазой В сети. Поэтому вектор Xi(b) должен быть направлен обратно вектору Х(В), ибо обмотки ВН и НН намотаны в разных направлениях. Наконец, для внутренней ветви зигзага оаи намотанной -на том же правом стержне, что и внешняя ветвь х\(b), должен быть построен вектор оаи совпадающий по направлению с вектором Х(В) обмотки ВН, а после перехода с одного стержня на другой по междуфазовому соединению промежуточных зажимов а\ и ух обход -по внешней ветви зигзага на среднем стержне даст вектор у\(а), направленный обратно вектору У (Л) обмотки ВН на среднем 36 стержне. Это построение показывает при совмещении центров фигур векторов, что после двойной одноименной перестановки группа 8 изменилась на группу 4, т. е. изменение группы было симметричным относительно оси 0—6 ч.
Такое же изменение группы произошло бы, если двойная одноименная перестановка была бы сделана с сохранением неизменного положения, например, обозначений фаз В и b, т. е. для обозначений в квадратных скобках на рис. 19. На самом деле для этих -преобразований -векторная диаграмма на стороне ВН осталась без изменения. Но вектор obi будет теперь направлен иначе, чем для ранее рассмотренного преобразования, для которого обозначения были взяты ранее в круглые скобки. Теперь для этой внутренней ветви зигзага, намотанной на среднем стержне, вектор напряжения определяется, исходя из направления вектора обмотки ВН на том же стержне, т. е. вектором У (В), и потому от точки о строим вектор оbь направленный влево вверх, тогда как ранее он был направлен влево вниз, как вектор Y(A).
Такое же изменение направлений векторов малой звезды для напряжений на внутренних ветвях зигзага получается и для -других ветвей. В частности, после построения вектора oai для внутренней ветви зигзага на нравом со стороны отводов НИ стержне вектор внешней ветви yi[b] дает положение конца вектора в точке [b], в точности соответствующее -положениям концов векторов b-и (b). Таким образом, получаем, что все три преобразования дали один и тот же результат — группа 8 перешла в группу 4.
То, что это преобразование не является простым преобразованием группы на —4 ч, показывает рис. 20, где Δ/А-10 переходит при помощи любого из трех преобразований в Δ/А-2, т. е. группа изменяется уже на +'4 ч. Фактически в отличие от циклических перемещений двойные одноименные перестановки преобразуют группу в симметричную относительно оси 0—6 ч. Как будет показано в дальнейшем, трупы 0 и 6 остаются при этих преобразованиях без изменения.
Рассматривая преобразования векторных диаграмм (риг, 201 для схемы Δ/Δ-10, замечаем, что, как это уже ранее пояснялось, перестановки двух фаз на стороне ВН приводят к указ шным ранее изменениям напра-в-
ления векторов треугольника ВН. После любой перестановки вектор обмотки, зажим которой обозначен либо А, либо [Л], либо (Л), всегда направлен горизонтально влево, на каком бы стержне ни была -намотана эта обмотка. В соответствии с этим все векторы ха, г [fa] и у (а) тоже направлены горизонтально влево и все промежуточные зажимы х, г, у этих векторов соединяются к концам другой обмотки, имеющим соответственно обозначения b, [b] и (b). Таким образом, положение и обозначение вершин равностороннего треугольника векторов НН остаются одинаковыми для всех трех двойных одноименных перестановок и совмещение центров треугольников векторов ВН и НН показывает, что после преобразований получаем схему Δ/Δ-2.

Рис. 21. Двойная одноименная перестановка для схемы Δ/Δ-6—> Δ/Δ-6.
Сопоставления преобразования схем (рис. 20 и 21), показаны на рис. 21. Из рис. 21 (для схемы Δ/Δ-6) следует, что двойная одноименная перестановка приводит к изменению группы на симметричное относительно оси 0—6 ч, а именно: двойная одноименная перестановка схемы Δ/Δ-6 приводит к той же схеме А/Δ-6.
Проследим построение векторной диаграммы для НН (рис. 21) для случая перестановки, когда обозначения фаз Л и а сохраняют свои положения, т. е. случай, когда новые обозначения записаны без скобок. Для обмотки 38
на .нравом стержне со стороны НН вектор ха должен быть нарисован в направлении, обратном вектору для обмотки ХА на стороне ВН, на левом стержне со стороны ВН, что учитывает разное направление намотки обмоток ВН и НН. После правого стержня со стороны НН обход совершаем по обмотке на левом стержне со стороны НН. На этом стержне, правом со стороны отводов ВН, намотана ZB, соединенная с фазой В сети ВН. Поэтому из конца а вектора ха строим вектор zb, направленный обратно вектору фазы В. Вершина b треугольника векторов НН заняла прямо противоположное положение по отношению к вершине В треугольника векторов ВН, т. е. получилась группа б.
Для группы 0 двойная одноименная перестановка двух фаз не приведет к изменению группы.
Если сопоставим системы расположения обозначений зажимов при двойных одноименных перестановках двух фаз. (рис. 17—21), то заметим, что это расположение сводится к трем системам: 1) АСВ\bса\ 2) CBA:abc\ 3) ВАС: cab при условии, что исходная система обозначений до преобразования была стандартной, .т. е. ABC: cba.
Обобщающие формулировки даны в приложении 3, разд. Б (б).
Двойные одноименные перестановки могут быть произведены и для схем, когда исходное расположение обозначений зажимов не соответствует стандартному. В основном это будут случаи двойных разноименных перестановок. Рассмотрим преобразование группы 3 в группу 9, которое является симметричным относительно оси 0—6 ч после двойной одноименной перестановки. Так как ни группа 3, ни группа 9 не могут быть получены при стандартном расположении обозначений зажимов, то преобразование группы 3 в группу 9 может рассматриваться как .промежуточное преобразование при двойной разноименной перестановке двух фаз.
В качестве примера рассмотрим (рис. 22) преобразование группы Y/A-7 (схема № 13 приложения 1) в группу Y/A-3. Это преобразование может быть получено различными путями. Можно путем циклических перемещений на стороне ВН или НН из группы 7 перейти в группу 3. Циклические перемещения на стороне НН должны быть произведены против часовой стрелки или на стороне ВН — по часовой стрелке. На рис. 22 по- казаны исходное соединение (обозначения в кружках) для схем У/Δ-7 и циклическое перемещение по часовой стрелке на стороне БН (обозначения в квадратных скобках). На стороне НН-обозначения в квадратных скобках сохраняются те же, что и исходные (в кружках), но, как показано в нижней половине рис. 22, группа 7 изменится на группу 3.
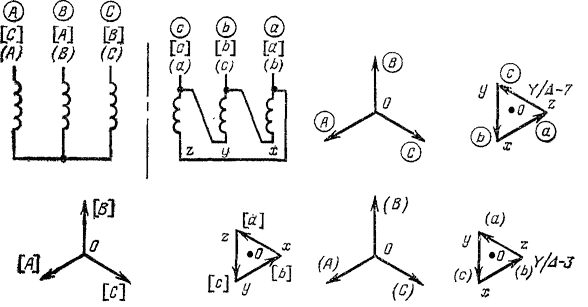
Рис. 22. Циклическое перемещение по часовой стрелке на стороне ВН или против часовой стрелки на стороне НН для схемы
Y/A-7—>-У/Δ-3.
На левом стержне со стороны НН находится обмотка фазы [с], а на соответствующем правом стержне со стороны ВН находится обмотка, соединенная с фазой В сети ВН. Так как обмотки ВН и НН намотаны в разные стороны, то вектор zjjc] должен быть направлен обратно вектору ВН фазы В, т. е. вертикально вниз. Далее от промежуточного зажима у обход совершаем по обмотке на среднем стержне, на котором намотана обмотка ВН фазы [Л]. Поэтому вектор у[b] построен в направлении, обратном вектору О [Л].
Подобным же образом можно проследить, что циклическое перемещение на стороне НН против часовой стрелки (обозначения в круглых скобках) тоже приведет к изменению исходной группы 7 на группу 3. Эти два циклических перемещения используются каждое отдельно для преобразования группы 3 в группу 9.
На рис. 23 как исходная (обозначения в кружках) используется схема Y/Δ-З на рис. 22, для которой обо- значения взяты в квадратные скобки. На рис. ЙЗ выполняются три двойные одноименные перестановки. Но в отличие от ранее показанных примеров одноименные обмотки (в исходном положении) намотаны на разных стержнях, т. е. фаза А на стороне БН присоединена к обмотке на среднем стержне, тогда как со стороны

Рис. 23. Двойная одноименная перестановка для схемы
Y/Δ-З—>Y/A-9.
НН на этом стержне намотана обмотка b и т. д. Тем не менее, сохраняется прежнее условие для перестановок: если фазы Л и а остаются на месте, то обозначения написаны без скобок, для фаз В и b, сохранивших свое исходное положение, обозначения взяты в квадратные скобки, а обозначения в круглых скобках относятся к случаю, когда фазы С и с сохранили свои места. Подробное построение векторной диаграммы НН для этого случая дано ниже.
На среднем стержне находится обмотка, вектор напряжения которой у (а) направлен вертикально вниз, поскольку при обходе в положительном направлении снизу вверх этот вектор у (а) должен иметь обратное направление по сравнению с вектором ОВ, ибо обмотки ВН и НН имеют разное направление намотки (разное направление дужек). Зажим а соединен с промежуточным зажимом х на правом стержне со стороны отводов НН. На том же левом со стороны отводов ВН
стержне находится обмотка, соединенная с фазой G сети ВН. Поэтому вектор х(b) должен быть построен в обратном направлении по отношению к вектору О(С). Достройка вектора г(с), обратно направленного по отношению к вектору О (Л), показывает, что после двойной одноименной перестановки фаз группа 3 перешла в группу 9. Аналогичный результат дают и две другие двойные одноименные перестановки, обозначения которых на рис. 23 взяты в квадратные скобки или написаны совсем без скобок.
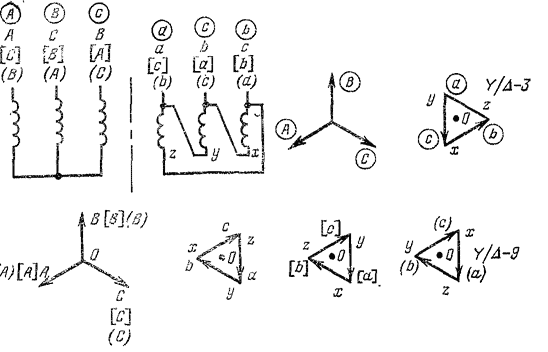
Рис. 24. Двойная одноименная перестановка для схемы
y/д-з— y/д-э.
На рис. 24 построены векторные диаграммы для трех двойных одноименных перестановок, для которых исходной является схема Y/A-3 на рис. 22 с обозначениями в круглых скобках.
Ниже дан пример построения векторной диаграммы НН для случая, когда обозначения зажимов на рис. 24 написаны без скобок. На левом стержне со стороны НН намотана обмотка га, а со стороны ВН—обмотка ОВ. Поэтому векторы ОВ и га параллельны, но направлены в разные стороны, поскольку обмотки ВН и НН имеют разное направление намотки. Зажим а соединяется с промежуточным зажимом у и обход по обмотке НН на среднем стержне даст вектор yb, направленный обратно вектору ОС обмотки ВН на среднем стержне. Замыкающий диаграмму вектор хс получаем при обходе обмотки на правом со стороны отводов НН стержне (левом со стороны отводов ВН), где находится обмотка ВН, соединенная с фазой А сети ВН. Таким образом, схема Y/Л-З перешла в группу 9, и это изменение группы справедливо и для других двойных одноименных перестановок, показанных на рис. 24 для обозначений в квадратных и круглых скобках.
На этом, однако, не заканчиваются возможные преобразования группы 7 по рис. 22 (схема № 13 приложения 1) в группу 9. Для разноименных двойных перестановок порядок преобразований не имеет значения. На рис. 22 показаны сначала циклические преобразования, а потом на рис. 23 и 24 — двойные одноименные преобразования. Теперь этот порядок изменяется — сначала выполняются три двойные одноименные перестановки (рис. 25), в результате которых группа 7 переходит в симметричную относительно вертикальной оси группу 5. Далее на рис. 26,а, б циклическими перемещениями группа 5 преобразуется в группу 9.
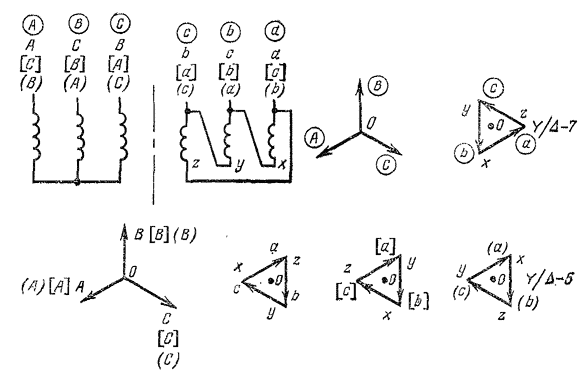
Рис.. 25. Двойная одноименная перестановка для схемы У/Δ-7—>-У/Δ-5.
При одноименных перестановках, показанных на рис. 25, исходное положение обозначений, взятых в кружках, является стандартным. Это преобразование особой новизны не имеет. Для полноты картины произведены все три двойные одноименные перестановки, для которых показаны обозначения без скобок, в квадратных и круглых скобках. На рис. 25 нанесены для ясности все положения промежуточных зажимов х, у, г.
Последующие циклические перемещения на стороне НН (рис. 26,а) весьма удобно сопоставлять с векторными диаграммами для обмоток НН (рис. 25). В этом случае циклическое перемещение обозначений по часовой стрелке на стороне НН для схемы Y/A-5 вполне очевидно дает группу 9 для всех трех схем Y/A-5 (рис. 25).

Рис. 26. Циклические перемещения по часовой стрелке на стороне НН для схемы Y/A-5—'"Y/A-9 и против часовой стрелки на стороне ВН для схемы Y/A-5->Y/A-9.
В этом случае положение обозначений на стороне ВН осталось без изменений.
Наоборот, на рис. 26,6 положение обозначений на стороне НН осталось без изменения по сравнению с рис. 25 и циклические перемещения произведены на стороне ВН против часовой стрелки, т. е. обозначение А ставится там, где раньше было обозначение С, В — на место А 1И С — на место В. При этом во всех трех случаях обозначения без скобок, в квадратных и круглых скобках не соответствуют стандартным. Обозначения всех промежуточных зажимов х, у и 2 на треугольниках векторных диаграмм НН позволяют легко осуществить построение всех этих диаграмм согласно сделанным ранее указаниям.
из них два циклических перемещения — всего 6 преобразований. Кроме того, выполнены еще шесть преобразований при обратном чередовании перемещений перестановок. Можно ожидать 12 различных систем обозначений, дающих преобразование группы 7 в группу 9.
Если сопоставим между собой все полученные результаты двойных разноименных перестановок (рис. 22, 23 и 26), то обнаружим, что имеется всего лишь три системы расположения обозначения зажимов: 1) ACB\abc\ 2) СБА : cab; 3) ВАС : bса.
На рис. 27 показано одно из возможных преобразований группы 7 в группу 1. Здесь за исходное расположение зажимов взято расположение, показанное в кружках и соответствующее группе 11, получающейся из группы 7 (рис. 22) путем циклического перемещения на -b4 ч по часовой стрелке. После этого сделаны три двойные одноименные перестановки, каждая из которых дала группу 1 (на рис. 27 обозначения без скобок, в квадратных и круглых скобках). Для большей наглядности на всех трех векторных диаграммах НН даны обозначения промежуточных зажимов х, у и г. Построение векторных диаграмм выполнено выше описанными способами.
Из рис. 27 следует, что предыдущие системы должны быть дополнены еще тремя системами расположения обозначений: 1) АСВ : cab-, 2) CBA:bca; 3) ВАС : abc.
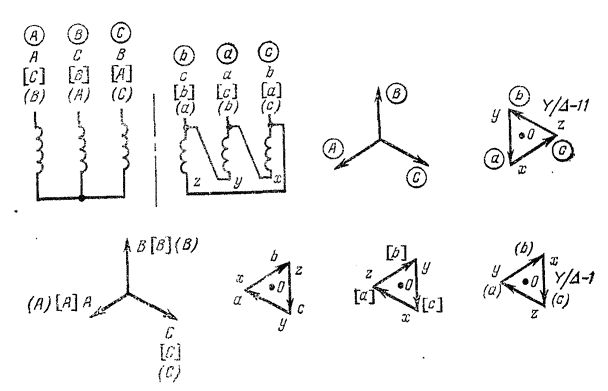
Рис. 27. Двойная одноименная перестановка после циклического перемещения У/|Δ-7+4-У/Δ-11-+Y/A-1.
Этим исчерпываются все возможные системы обозначений, которые могут быть получены при двойных разноименных перестановках, если исходное расположение зажимов было стандартным.
В приложении 3, раздел В, сформулированы общие результаты для двойных разноименных перестановок. Эти выводы получены путем многочисленных преобразований различных нечетных схем соединения. В строках 18—23 даны 2 раза три двойные разноименные перестановки, различающиеся тем, что для строк 18—20 сначала производят циклические перемещения на +4 ч, а потом делают двойную одноименную перестановку из нестандартного расположения обозначений. Этот порядок преобразований описан в столбце «Вид и порядок преобразований». Численные изменения групп показаны в следующем столбце. Каждая из строк 18—20 может быть использована для преобразования любой из четырех групп: 11, 5, 1 и 7, показанных в этом столбце. В этом столбце прибавление +4 ч означает соответствующее циклическое преобразование, безразлично на стороне ВН или НН, а далее стрелка обозначает двойную одноименную перестановку фаз.
Следующие строки 21—23 дают тот же конечный результат изменения групп, получающийся при иной последовательности преобразований — сначала двойная одноименная перестановка, а потом циклическое перемещение на —4 ч. Поэтому в столбце «Изменение группы в часах» сначала показана стрелка для двойной одноименной перестановки, а потом число часов уменьшено на 4 ч как результат циклического перемещения.
В первой половине таблицы на стороне ВН сохраняет свое положение обозначение фазы А в строках 18 и 21, фазы В для строк 19 и 22 и фазы С для строк 20 и 23, на стороне НИ сохраняют соответственно обозначения фаз с, а и b. Во второй половине таблицы на стороне НН на соответствующих строках сохраняют положение обозначения фаз b, с и а и сохраняется предыдущая система обозначений фаз ВН. Эта новая система расположения обозначений фаз НН получается при иной последовательности преобразования, указанной в столбце «Вид и порядок преобразований», и дает иной результат изменения групп по сравнению с первой половиной таблицы.
При практическом использовании результатов разноименных перестановок, например при необходимости преобразовать группу 1 в группу 7, вовсе не следует повторять все промежуточные построения, указанные в столбце «Вид и порядок преобразований». Эти преобразования имеют расчетный характер, и потому можно сразу соединить левые, средние и правые зажимы со сторон ВН и НН с теми же фазами сети А, В, С, с, b, а, как указано в любой из строк 18—20, или по любой из граф 21—23 в том случае, если исходное положение обозначений для схемы, например с группой 1, было стандартным.
Таблицы приложения 3 показывают также, что любая нечетная группа может быть преобразована в любую другую нечетную группу. Если взять группы 1 и 11 как исходные, то путем циклических перемещений на ±4 ч можно получить два ряда нечетных групп: 1, 5 и 9; 11, 7 и 3.
Двойные одноименные перестановки преобразуют нечетные группы в симметричные относительно оси 0—6 ч.
Наконец, двойные разноименные перестановки позволяют сделать остальные преобразования нечетных групп, например группы 1 в группу 7 (строки 18—23 приложения 3, раздел В) я в группу 3 (строки 24—29). Аналогично можно проследить возможность преобразования любой нечетной группы в любую другую, причем это можно достичь при помощи трех различных систем положений обозначений зажимов.
Для одноименных и разноименных перестановок три различные системы положений обозначений зажимов получаются из-за трех возможностей сохранить неизменным положение одной из фаз, а для циклических перемещений, как это видно из разд. А (а) и А (б) приложения 3, три возможные системы расположения зажимов получаются из возможности сделать циклическое перемещение либо на стороне НН, либо на стороне ВН, либо на той и другой сторонах одновременно. Например, циклические перемещения на +4 ч для преобразования группы 11 в группу 3 можно сделать по строке 1 приложения 3 для циклического перемещения на стороне
МП либо по строке 4 для циклического перемещения по стороне ВН, либо по строке 5 для циклического перемещения на сторонах ВН и НН. В результате получаются следующие три возможных расположения обозначений зажимов: 1) АВС:bас; 2) ВАС : cba; 3) CAB : acb.
В разд. Б (б) приложения 3 для двойных одноименных перестановок показаны в строках 12—14 преобразования четных групп в симметричные относительно оси О—6 ч. Однако в разделе В указаны двойные разноименные перестановки только для нечетных групп. Для четных групп двойные разноименные перестановки не приведены, так как они особого интереса не представляют. Двойные одноименные перестановки для четных групп дают изменение группы либо на +4 ч, либо на —4 ч, смотря по положению исходной группы IB той или иной четверти круга; в первой и третьей четвертях круга изменение происходит на —4 ч, а во второй и четвертой—на + 4 ч. Двойные разноименные перестановки являются комбинацией двойной одноименной перестановки и циклического перемещения, т. е. могут отличаться от двойной одноименной перестановки лишь на ±4 ч.
Поэтому если разбить все четные группы путем последовательных циклических перемещений на два ряда: О—4—8 ч; 6—10—12 ч, то согласно предыдущим соображениям можно заключить, что не могут быть получены преобразования четной группы одного ряда в четную группу другого ряда. При двойных одноименных перестановках группы 4 и 8, а также 10 и 2 находятся в пределах своих рядов, а группы 0 и 6 остаются неизменными.
Такие же двойные разноименные перестановки по строкам 18—20 приложения 3, при которых, например, группа 4 путем циклического перемещения на +4 ч переходит в группу 8, а -потом путем двойной одноименной -перестановки возвращается в ту же группу 4, очевидно не могут получить широкого распространения. Группа 4 по строкам 24—26 может быть преобразована сначала в группу 0, а потом после одноименного двойного перемещения сохранить группу 0.
Оба эти преобразования показаны на рис. 28 и 29 без промежуточных построений. На рис. 28 в качестве исходной взята схема № 23 приложения 2 (обозначения в кружках) и сразу проставлена система обозначений по строке 19 приложения 3 (обозначения без скобок).
В этом случае группа не должна измениться, что и показано на векторных диаграммах после преобразований. Совмещение диаграммы показывает, что после преобразования группа 4 не изменилась.

Рис. 28. Двойная разноименная перестановка, при которой схема A/Z-4—>-A/Z-4, т. е. группа не изменяется.

Рис. 29, Двойная разноименная перестановка, при которой схема Л/А-4—'"Δ/Δ-О.
На рис. 29 в качестве исходной была взята схема № 7 приложения 1 (обозначения в кружках). Далее были сразу записаны обозначения по строке 26 приложения 3 и, как сказано выше, должна была получиться
группа 0. Это подтверждается контрольным построением векторных диаграмм.
Итак, четная труппа не может быть преобразована в нечетную группу и наоборот. При перепайке соединений обмоток внутри трансформатора изменяется его коэффициент трансформации и потому у трансформатора с четной группой нельзя путем пересоединения зажимов добиться того, чтобы он работал в параллель с трансформатором нечетной группы и наоборот.
Предыдущий обзор охватывает все основные простые преобразования групп и ряд комбинированных преобразований, имеющих решающее значение при оценке возможности параллельной работы трансформаторов.


