А.Т. ДЕМЧУК, И. Й. ШТЕФКА ОАО «СО ЕЭС»1, ОАО «НИИПТ»2
Россия shtefka y@niipt.ru
КЛЮЧЕВЫЕ СЛОВА
Энергосистема, спектральный анализ, метод Прони
Спектральные методы исследования случайных сигналов давно известны, и хорошо разработаны. С их помощью можно не только описывать процессы, протекающие в энергосистемах, но и вырабатывать рекомендации по улучшению качества функционирования этих энергосистем. С другой стороны, корректное применение спектральных методов применимо только к классу стационарных случайных процессов неограниченной длительности. Реальные процессы в энергосистемах имеют нестационарный характер, поэтому для определения динамически изменяющегося спектра процесс надо разбивать на отрезки, и для каждого отрезка спектр вычислять отдельно.
С уменьшением длительности отрезка увеличивается ширина разрешающей полосы, что затрудняет идентификацию близко расположенных частот, и снижает точность определения самих частот. Выбор перекрывающихся отрезков, увеличивает количество полученных спектров. Это позволяет улучшить полученные результаты.
При анализе процессов, которые имеют место в энергосистемах, зачастую важно знать не полную спектральную плотность мощности, а отдельные колебательные составляющие, обусловленные протекающими в системе процессами, такими, как низкочастотные колебания. Непрерывная часть спектральной характеристики в таком случае ассоциируется с помехой.
В настоящее время все чаще используются методы частотного анализа, не использующие преобразование Фурье. Одним из них является метод Прони, основанный на представлении аппроксимации исследуемого процесса детерминированной экспоненциальной моделью. Метод позволяет непосредственно выделить отдельные колебательные составляющие процесса, определить их частоту и амплитуду. По полученным составляющим сигнала можно восстановить процесс, и определить погрешность разложения.
В докладе рассмотрены некоторые факторы, влияющие на точность оценки параметров колебательных составляющих процессов, полученных с помощью метода Прони.
Для оценки эффективности метода, следует в качестве тестового процесса использовать сигнал с известными параметрами. Простейшим процессом, моделирующим колебательный процесс с переменной частотой, является линейно развернутая синусоида. Ее частота изменяется в заданных пределах линейно. Были сформированы два тестовых процесса. Первый процесс содержит одну развернутую синусоиду с единичной амплитудой, частота которой за 200 секунд изменяется от 0.1 Гц до 1 Гц, т.е. частота изменяется со скоростью 5 мГц/с. Второй процесс состоит из двух развернутых синусоид со встречным направлением изменения частоты. Частота первой синусоиды изменяется от 0.1 Гц до 1 Гц, второй - от 1 Гц до 0.1 Гц, за те же 200 секунд. Функции заданы дискретно с интервалом дискретизации 20 мс, который характерен для данных, полученных с помощью СМПР. График второго процесса показан на рис. 1.
При обработке процесс сканируется скользящим окном заданной длительности. Результаты расчета для каждого окна соотносятся с моментом времени, соответствующему середине этого окна. При этом каждый рассчитанный параметр (частота, амплитуда, и т.д.) может быть представлен в виде функции времени, и выведен на график. Данные по величине спектральной мощности представлены в виде квадратного корня этой величины, что соответствует амплитуде спектральной составляющей.

Рис. 1: Тестовый сигнал, состоящий из двух развернутых синусоид
Метод Прони позволяет получить амплитуды, частоты, декременты затухания и фазы всех составляющих процесса. Рассмотрение данного метода удобно начать с процесса, состоящего из одной линейно развернутой синусоиды.
На рис. 2 показана зависимость двух частот, вычисленных методом Прони для окна 5 с, от времени. Наблюдается большой разброс показаний в начале и заметное отклонение рассчитанных частот от истинного значения. На рис.3 приведены амплитуды полученных колебаний. Видно, что сумма значений амплитуд приблизительно равна амплитуде исходной развернутой синусоиды.

Рис. 2: Частота колебаний, выделенных методом Прони для окна 5 с.
На рис. 4 показаны соответствующие декременты затухания. В области устойчивых значений декременты имеют разные знаки. Полученный результат можно объяснить тем, что на каждом выделенном окном отрезке развернутая синусоида представлена двумя синусоидами: одной - затухающей, аппроксимирующей процесс в начале окна, другой - возрастающей - в конце. В сумме эти синусоиды близки к исходному процессу. Низкая точность метода в начале процесса обусловлена тем, что в этой области высока относительная скорость изменения частоты. Так, за время первых 5-ти секунд частота изменяется на 25%. При такой скорости изменения частоты двух синусоид недостаточно для удовлетворительной аппроксимации. Использование же большого числа аппроксимирующих членов противоречит смыслу задачи.

Рис. 3: Амплитуда колебаний, выделенных методом Прони для окна 5 с.

Рис. 4: Декремент затухания колебаний, выделенных методом Прони для окна 5 с.
Похожая ситуация возникает при увеличении длины окна. На рис. 5 приведена относительная погрешность метода Прони при расчетах с окнами разной длительности. Для длинных окон двух затухающих синусоид недостаточно для хорошего приближения.
Аналогичные расчеты были выполнены для процесса с двумя развернутыми синусоидами, показанном на рис. 1. На рис. 6 и 7 приведены графики частоты и амплитуды. Небольшое смещение частоты есть и в этом случае, хотя оно меньше значения для процесса с одной развернутой синусоидой. Так же наблюдается увеличение погрешности в области низких частот. Амплитуда составляющих соответствует амплитудам развернутых синусоид процесса. Декремент затухания близок к нулю. Метод имеет конечную разрешающую полосу, и близкие по частоте составляющие сигнала неразличимы. Рассчитанные значения могут в этом случае сильно отличаться от действительных значений.
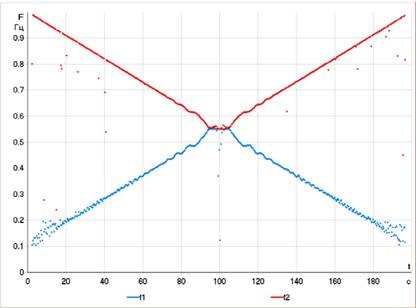
Рис. 6: Частота колебаний, выделенных методом Прони для окна 5 с.

Рис. 5: Погрешность метода Прони для окон разной длительности (5с, 10с, 20с и 50с)
При анализе реальных процессов всегда существует заметная составляющая шума. Как правило, для удовлетворительных результатов анализа, недостаточно только удалить тренд сигнала и отдельные выбросы. Желательно с помощью полосовых фильтров предварительно выделить диапазон частот, в котором расположены интересующие колебания. В качестве реального процесса взята частота напряжения на шинах Харанорской ГРЭС при отключении
блоков № 3, 4 на Балаковской АЭС (2000 МВт) 04.05.2007. Кривая изменения частоты показана на рис. 8.
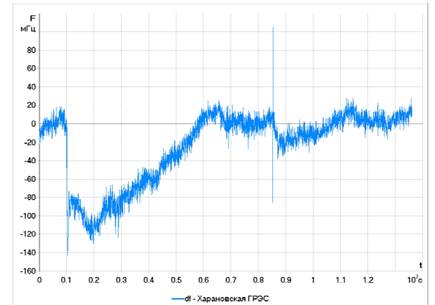
Рис. 8:Частота напряжения на шинах Харанорской ГРЭС

Рис. 7: Амплитуда колебаний, выделенных методом Прони для окна 5 с.
На рис.9 - сравнение этого процесса с кривой после фильтрации полосовым фильтром 0.1-0.8 Гц.
Один из параметров метода Прони - число комплексных экспонент g, входящих в разложение. Значению g соответствует разложение на g/2 затухающих синусоид. Считается, что чем этот параметр больше, тем точнее приближение к исходному процессу. Такой подход справедлив, если по данным разложения предполагается строить спектральную плотность распределения мощности. Если же нужно выделить основные колебательные составляющие процесса, целесообразно ограничиться небольшим количеством слагаемых. Минимальное число комплексных компонент - g=2. Это соответствует поиску единственной колебательной составляющей.

Рис. 9: Сравнение процесса рис.8 до и после фильтрации фильтром 0.1-0.8 Гц (сегмент)
На рис. 10 показан результат обработки методом Прони с g=2 отфильтрованной частоты напряжения Харанорской ГРЭС для окон трех размеров - 5 с, 10 с и 20 с.

Рис. 10: Частота колебательных составляющих процесса для g=2 и окон 5 с, 10 с и 20 с.
Чем шире окно, тем меньше разброс показаний. На рис. 11 результаты разложения для разных значений g сравниваются друг с другом и со случаем g=2.
На рисунке показаны первые две колебательные составляющие для каждого значения g (кроме g=2). Кривые, относящиеся к одному расчету, выведены одним цветом. При разложении на две колебательные составляющие (g=4) видно, что ни одна из полученных составляющих не совпадает с исходной кривой, вычисленной для g=2. Более близкая по значениям составляющая сдвинута в сторону низких частот по отношению к исходной кривой (g=2). Вторая колебательная составляющая расположена заметно выше первой в области верхней частоты среза фильтра. При увеличении числа компонент, рассматриваемые две компоненты, постепенно сдвигаются в сторону увеличения частоты, так что в определенный момент (для данного процесса при g=8) обе оказываются выше исходной кривой. В этот момент в результатах расчетов возникает вычислительная неустойчивость, проявляющаяся в возможном скачкообразном изменении частот колебательных составляющих. Пример такого явления приведен на рис. 12.
С увеличением числа компонент в разложении на экспоненциальные составляющие вероятность и частота таких скачков увеличивается. Вопрос в том, отображает ли указанное явление реальные процессы, протекающие в энергосистеме.

Рис. 12: Скачкообразное изменение частот колебательных составляющих (окно 20с)

Рис. 11: Частота колебательных составляющих процесса при g=2, 4 и 8 для окна 20 с.
На рис.13 представлены амплитуды рассматриваемых на рис.12 процессов совместно с кривой исходного процесса после фильтрации, на рис. 14 - соответствующие декременты затухания. Как видно из рис.13, амплитуды двух колебательных составляющих, полученных методом Прони с 9-ью компонентами, существенно превышают амплитуду исходного процесса. С другой стороны, затухание увеличивается до такой степени, что значения компонент в конце окна практически равны нулю. Отсюда следует, что вычисленные составляющие аппроксимируют сигнал только в начале окна, а значения сигнала в конце окна полностью попадают в погрешность. Такое возможно потому, что общая относительная погрешность аппроксимации превышает в рассматриваемом случае 80%.

Рис. 13: Сравнение амплитуд колебательных составляющих (окно 20с) с исходным процессом
При использовании метода Прони с выделением двух компонент (рис. 11), частота второй компоненты оказалась в области спада амплитудной характеристики фильтра. Достоверность такого результата мала. Для уточнения надо повторить расчеты с фильтром, не искажающим сигнал на интересующей частоте.
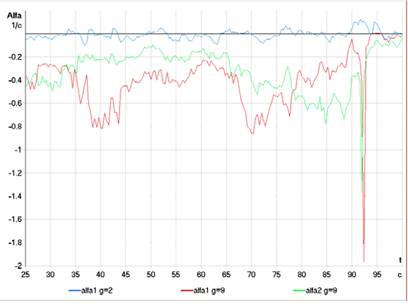
Рис. 14: Декременты затухания колебательных составляющих (окно 20 с) при разных g
Проведенный анализ показывает, что при использовании метода Прони следует проявлять осторожность, так как параметры колебательных процессов, полученные с помощью этого метода, сильно зависят от условий расчета. В результате могут появиться дополнительные колебательные составляющие, которых нет в исходном процессе. С другой стороны, аналогично остальным методам спектрального анализа, существует конечная разрешающая полоса, вследствие которой компоненты, отличающиеся друг от друга на 0.1 - 0.2 Гц не могут быть идентифицированы как отдельные сигналы.
Достоинство метода Прони в том, что позволяет легко получить доминирующие колебания процесса. Для повышения достоверности результатов следует предварительно
выделить с помощью симметричного полосового КИХ-фильтра сигнал требуемого частотного диапазона, и использовать метод Прони с разложением на число компонент, равное или немного превышающее ожидаемое число колебательных составляющих в рассматриваемом частотном диапазоне. Для повышения точности следует, по возможности, сужать полосу фильтрации. При необходимости можно формировать несколько частично перекрывающихся диапазонов.
ЛИТЕРАТУРА
- С.Л. Марпл мл. Цифровой спектральный анализ и его приложения. М.: Мир, 1990.
- H. Breulmann, W.Winter, R. Witzmann, P. Dupuis, M.P. Houry, T. Margotin, J. Zerenyi, J. Dudzik, J. Machowski, L. Martin, J. M. Rodriguez, E. Urretavizcaya. Analysis and Damping of Inter-Area Oscillations in the UCTE/CENTREL Power System. www.ucte-ipsups.org/Pdf/Download/englisch/CIGRE38113.pdf


