Потери на транзит электроэнергии и их распределение между участниками энергообмена

Толасов А. Г.
Первоначальная идея принадлежит Холостову С. В. (Ленэнерго) и Тимченко В. Ф. 

Под транзитом электроэнергии понимается ее передача между участниками энергообмена, не имеющими общих электрических границ и связанными посредством “буферных” сетей прочих участников параллельной работы. Несмотря на то, что для последних такая передача имеет сквозной характер, они несут расходы по обслуживанию и ремонту своих транзитных сетей и в силу действующей инструкции [1] на их баланс списываются потери энергии от этих транзитных перетоков. В целях обоснования взаиморасчетов между получателями электроэнергии и владельцами транзитных сетей необходимо решить по меньшей мере две задачи:

1. определить (оценить) общий объем транзитных потерь в сети;
2. распределить его между участниками энергообмена.

Первая задача имеет очень простое решение, если при известном полном объеме потерь в сети сначала рассматривается задача 2.
Распределение потерь между участниками рынка энергии и мощности. Метод передаточных коэффициентов. Рассмотрим простейшую схему транзита электроэнергии (рис. 1). Энергосистемы I и 2 покрывают свой дефицит мощности (энергии) внешним перетоком от избыточной ЭЭС 3 через “пассивную” сеть с эквивалентным сопротивлением Zc. В ней отсутствуют собственные источники генерации и нет промежуточных отборов. Полагаем известными перетоки W\, W2, W3 и потери в сети AW.

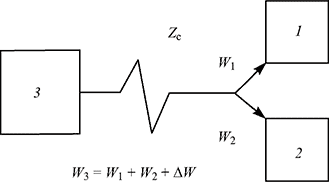
Рис. 1. Схема простейшего транзита электроэнергии

Объем последних в данном случае будет совпадать с объемом потерь на транзит. Для простоты положим, что указанные перетоки являются перетоками активной мощности, хотя принципиальных трудностей для того, чтобы оперировать комплексными величинами или их модулями, не существует. Подчеркнем, что получатели электроэнергии (для начала) находятся в совершенно одинаковых условиях: обоих снабжает один и тот же поставщик, получение энергии происходит с одних и тех же шин. Покажем, что для определения потерь каждого партнера в этом случае не требуются проведение режимных расчетов и знание параметров сети.
Транзитные нагрузочные потери в сети Zc в каждый момент времени пропорциональны выражению
(1)
Отсюда видно, что потери каждого получателя определяются квадратом его собственного перетока, а также частично общим перетоком 2WW2. Следовательно, можно сказать, что для случая рис. 1 вторая из сформулированных ранее задач сводится к распределению между адресатами перетоков линейного члена 2 WW2. Разделив последний на части, пропорциональные составляющим его величинам W1 и W2
(2)
можем определенно указать на потери, за которые “несет ответственность” первый или второй участник,
(3)
где индексом i обозначен номер интересующего нас получателя транзита, а индексом j - номер его партнера. Избавиться от неизвестного Zc можно, поделив уравнение (3) на (1). В результате получим выражение доли потерь i-го получателя в общих потерях на транзит
(4)
На рис. 2 показана зависимость доли потерь (4) одного из двух участников энергообмена от доли перетока этого участника в суммарном транзитном перетоке dWi = Wi/(Wi+ Wj).

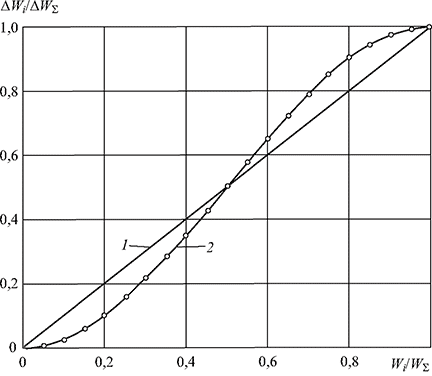
Рис. 2. График зависимости доли потерь одного из двух партнеров от доли его перетока в суммарном при одинаковых условиях транзита (2):
1 - биссектриса координатного угла

Отклонение построенной долевой зависимости от координатного угла показывает большую или меньшую степень “виновности” данного участника энергообмена в образовании общих потерь на транзит. Можно отметить, что оплата транзита электроэнергии получателями по одинаковому тарифу, несмотря на, казалось бы, совершенную очевидность, так как они находятся в равных условиях, на самом деле обоснована только в случае приблизительного равенства их перетоков. Если же, например, переток одного из партнеров составляет 20% суммарного, то, как можно видеть, транзит необходимой энергии обойдется ему вдвое дороже, чем это есть на самом деле. Такая же тенденция имеет место и для большего числа партнеров.
На рис. 3 показано семейство кривых, описывающих долю потерь одного из трех партнеров (5) при постепенном долевом нарастании его перетока в суммарном. При этом величина перетока какого-либо из двух оставшихся партнеров определенным образом фиксируется, например, на уровне 50, 40 или 30% суммарного перетока.
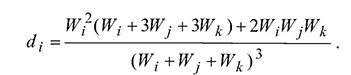(5)
Естественно, уравнение (1) можно обобщить на произвольное число партнеров п. Выражение доли потерь каждого из них тогда примет следующий вид:
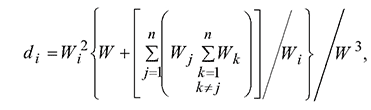(6)

где- сумма перетоков всех участников.
Распределение потерь согласно выражению (6) может с успехом применяться в случае, когда сеть Zc представлена всего одним элементом: линией электропередачи или трансформатором. Описанный подход также можно считать применимым, если:

1. “точки транзита” в сложной сети (т.е. узлы, куда поступают и откуда снимаются потоки энергии) для всех участников совпадают или электрически близки по сравнению с маршрутом транзита;
2. собственная генерация и потребление в сети, по которой осуществляется транзитный оборот, существенно меньше объема транспортируемой энергии и первыми можно пренебречь;
3. соблюдается одновременность замеров исходных величин или иная синхронность в их сборе.

В реальных сетях указанные требования чаще всего не соблюдаются, за некоторым исключением для условия 3.
Усложним первоначальную задачу. Пусть получатели транзита имеют различную электрическую удаленность от узлов поступления энергии в сеть Zc. Если бы для каждого рассматриваемого момента (периода) времени были известны оценки входных сопротивлений сети относительно интересующих нас точек транзита, то методом “активного двухполюсника” упрощенно можно было бы без особенных трудностей вычислить потери для каждого получателя транзита.
Чем меньше электрическая удаленность генерирующих узлов от выбранной точки (сечения), тем меньше входное сопротивление относительно него и соответственно меньше удельные потери на передачу электроэнергии. Следовательно, “удаленность” транзита энергии для каждого получателя могла бы определяться соотношением мгновенных или усредненных значений входных сопротивлений сети относительно узлов получения электроэнергии. Недостаток такого способа заключается в трудоемкости определения входного сопротивления активной (с источниками генерации) сети. Возможность натурных замеров маловероятна, теоретические расчеты сложны, требуют знания параметров всех электросетевых элементов и узловых токов в схеме замещения. При этом достоверность расчетов становится весьма условной.
Как можно решить данную задачу, не прибегая к этому или другим трудоемким методам? Представим сложную сеть с позиций принципа “черного ящика”, в соответствии с которым изучение любого объекта не связано с вопросом об его внутреннем устройстве, - достаточно выяснить характерные реакции на заданные внешние воздействия, т.е. определить его передаточные функции. Входными величинами для нашей исследуемой системы являются транзитные перетоки энергии, выходными - потери на транзит.
Получение передаточных функций сети физически будет соответствовать следующей постановке вопроса: “Как соотносятся потери участников энергооборота, если величины их транзитных перетоков в фиксированный момент времени одинаковы?” Ответ будет также характеризовать относительную электрическую удаленность участников энергообмена друг относительно друга. Передаточные функции в реальных сетях могут быть получены при помощи отработанного математического аппарата, описанного, например, в [2]. Рассмотрим, что для этого необходимо.
В матричном виде реакция динамической системы на внешнее воздействие может быть записана как Y(t) = H(t)X(t). Допустим, что с учетом:
линейности токов друг относительно друга;
единовременности замеров исходных параметров и/или одинаковости интервалов времени, на которых они суммируются или усредняются;
Таблица 1
Численные оценки передаточных коэффициентов сетей различных классов номинального напряжения АО Ленэнерго по потерям на транзит для участников рынка оборотов энергии

постоянства местоположения точек транзита и мест замеров параметров,

Рис. 3. График зависимости доли потерь одного из трех партнеров от доли его перетока в суммарном при одинаковых условиях транзита:
доля потерь одного из двух оставшихся партнеров фиксировалась в объеме: 1 - 90% суммарного перетока; 2 - 80%; 3 - 70%; 4 - 60%; 5 - 50%

Рис. 4. График характерных изменений вариации нагрузочных потерь электроэнергии в зависимости от объема (доли) произвольно выбранной части сети:

потери взяты в долях суммарных; данные эквивалентированной сети ВЛ 330 кВ АО Ленэнерго за 1994 - 1997 гг.

выражение (1), обобщенное на п получателей транзита, может быть записано так
(7)
где H=(h1 ... hn) - вектор-столбец передаточных функций сети, которые, как уже говорилось, при равенстве транзитных перетоков отражают электрическую разноудаленность точек транзита от источников поступления энергии в сеть.
Пренебрегая (на первом этапе) различием напряжения в разных точках сети и учитывая названные факторы, можно отметить, что эти передаточные функции должны являться практически постоянными величинами. Поэтому далее их будем называть передаточными коэффициентами.
Пусть в результате каких-либо мероприятий нам известен вектор Н значений передаточных коэффициентов рассматриваемой сети для всех п участников рынка оборотов энергии. Тогда по аналогии с получением формулы (6) можно вывести выражение доли потерь i-го участника в суммарных транзитных потерях
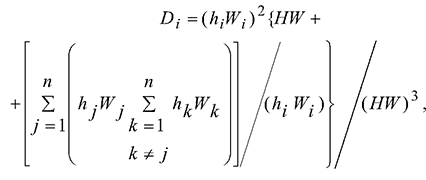(8)
где 1- сумма перетоков всех участников со своими передаточными коэффициентами.
Применение выражения (8) позволит, таким образом, кардинально решить проблему; транзитные потери энергии будут распределяться, во-первых, в зависимости от электрической удаленности всех заинтересованных сторон от источников поступления энергии в сеть; во-вторых, в рассмотренной зависимости от доли их перетоков в суммарном.
Владелец сети рассматривается как еще один участник рынка оборотов в дополнение к собственно получателям транзита. Этим достигается решение первой поставленной задачи об определении общего объема потерь на транзит.
Сначала суммарные отчетные потери распределяются между всеми участниками рынка оборотов электроэнергии, включая владельца сети, затем из полученных компонент находится сумма потерь истинных участников транзита. Таким образом, определение потерь на транзит базируется на стандартной процедуре получения обычных отчетных потерь; осуществляется с той же точностью и периодичностью; не зависит от дополнительной информации.
На базе данной методики также может быть представлена количественная оценка того, в какой мере снабжение выбранного потребителя осуществляется за счет поступления от смежных ЭЭС, трансформацией из других классов напряжения, собственной генерацией в сети данного Uном и т.д. Для этого в качестве исходных данных будут затребованы другие величины, подход останется прежним.

Получение передаточных коэффициентов транзита в реальной сети.

При выводе формул (4) - (8) сопротивление сети Zc не имело никакого значения (сокращалось в процессе вывода). Также сократится любой отличный от нуля множитель, стоящий на его месте. Следовательно, применительно к нашей задаче, т.е. при получении долей, можно в выражениях (7) - (8) “заранее”, если так можно выразиться, сократить все постоянные множители и вместо знака пропорциональности поставить знак равенства. Извлекая из обеих частей (8) квадратный корень, получим следующее выражение:
(9)
где правая часть является аналитическим представлением множественной линейной регрессии без нулевого члена, а параметры h1 ... hn последней могут интерпретироваться как коэффициенты чувствительности функции потерь к изменению того или иного транзитного перетока.
Вычисление неизвестных параметров формулы (9) - обычная задача регрессионного анализа, однако в данном случае вычисляются не абсолютные значения параметров регрессии, а ее, так называемые, частные коэффициенты (ЧКР), основное свойство которых - численная оценка степени влияния того или иного аргумента. Не вдаваясь в подробности, отметим, что получение ЧКР - стандартная процедура специализированного математического обеспечения ПЭВМ, описание которой также можно найти, например, в [2].
В табл. 1 на примере сети АО Ленэнерго для укрупненных получателей транзита по отчетным данным структуры баланса 1995 - 1997 гг. приводятся расчетные значения передаточных коэффициентов транзита. Как можно видеть, качество подгонки регрессионных моделей является довольно высоким, а дополнительные исследования подтвердили высокую временную стабильность их параметров.
Расчеты потерь электроэнергии при транзите на основании данной методики в информационных целях проводились на протяжении ряда лет в сетях региона Ленэнерго и показали, что распределение потерь между РАО и АО, осуществляемое согласно [1], не соответствует действительности.