Эффективность кода определяется, в частности, избыточностью, т. е. долей контрольных символов к по отношению к информационным и„ при обеспечении заданной помехозащищенности кода. Собственно искусство кодирования и состоит в выборе таких методов, которые обеспечивают при равной помехозащищенности меньшую избыточность кода. Особенно это важно для быстродействующих систем передачи сообщений, где приходится экономить на времени каждого дополнительного контрольного бита.
Одним из методов повышения эффективности кодирования является использование коррелированности сообщений в определенной зоне их значений. К этому методу, в частности, относится метод построения без избыточных кодов, помехозащищенных в зоне передаваемых сообщений [23].
Этот метод является развитием метода проф. Г. М. Бутаева при передаче медленно меняющихся ТИ, основанного на том, что каждое последующее значение ТИ не должно отличаться от предыдущего более чем на 1 квант. При этом кодирование соседних значений ТИ обеспечивается без избыточным кодом с заданным кодовым расстоянием d >2 [21].В этом смысле без избыточный код приобретает свойства помехозащищенного кода.
Таблица 3.17. Зависимость т (h ) и допустимые отклонения
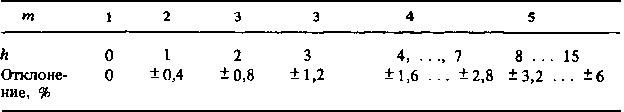
В телеинформационных системах реального времени последовательные отчеты телеизмерений (ТИ) технологических процессов обычно сильно коррелированны. Это обстоятельство позволяет применить метод семантического контроля при приеме ТИ [22]. Суть его состоит в том, что контролируется правильность приема кодового слова только в определенной зоне (апертуре), которая устанавливается вокруг последнее го переданного значения. В соответствии со статическими характеристиками источника сообщений появление соседних отсчетов, отличающихся друг от друга более чем на h квант, мало вероятно и квалифицируется как ошибка при передаче*.
Каждое сообщение порождает свою зону разрешенных значений Y, которые удовлетворяют условию![]() , где х — принятое ра
, где х — принятое ра
нее значение ТИ. Кодовое расстояние d > 1, обеспечивающее помехоустойчивое кодирование, должно соблюдаться не для всего множества кодовых слов, а лишь для кодовых слов, входящих в контролируемую зону.
Пусть формат без избыточного двоичного кода содержит п разрядов, величина апертуры содержит 2h + 1 уровней квантования. Исходные кодовые слова в пределах апертуры отличаются лишь т младшими разрядами, число которых связано с h следующей зависимостью:
![]() (3.23)
(3.23)
откуда
![]()
Зависимость необходимого числа т для обеспечения заданной апертуры h и соответствующие отклонения параметра при 8-разрядном исходном коде приведены в табл. 3.17.
Защите подлежат только т младших разрядов исходного кода, а искажения в n—т старших разрядах обнаруживаются апертурным контролем.
Защитные разряды к=n—т ставятся в соответствие т информационным разрядам, обеспечивая заданное кодовое расстояние для кодовых комбинаций из младших разрядов. При этом защитные разряды совмещаются со старшими информационными разрядами путем суммирования с ними по модулю 2.
При декодировании осуществляется обратная операция: по т младшим разрядам принятого слова вычисляются защитные к разрядов, которые суммируются по модулю 2 с n — т старшими разрядами принятого кода. В результате суммирования образуются старшие информационные разряды принятого сообщения.
Рассмотрим предлагаемый метод кодирования на примерах линейных (и, т) -кодов, которые могут быть представлены образующей матрицей G (n, т). Контрольные к разрядов записываются для т единичных векторов, образующих верхние строчки матрицы. Остальные n— т строчек соответствуют незащищенным старшим разрядам, которые при формировании кодовых слов накладываются на к защитных разрядов суммирования по модулю 2.
Определение к защитных разрядов для т младших разрядов, которые играют роль информационных разрядов в линейном коде, производится любыми известными способами синтеза помехозащищенных линейных кодов, например выбором соответствующих образующих полиномов для циклических кодов.
В соответствии с известными границами Хэмминга—Плоткина [16] (n, m)-код может обеспечить кодовое расстояние не более d' для всех значений кодовых слов, входящих в зону апертурного контроля, только в том случае, когда в пределах зоны старшие разряды сохраняются неизменными. Если же в общем случае внутри зоны есть изменение старших разрядов (всегда не более одного кванта), то это может привести к уменьшению кодового расстояния. Для того, чтобы это уменьшение не превосходило 1, предлагается старшие разряды кодировать кодом Грэя. При этом во всех контролируемых зонах обеспечивается кодовое расстояние не менее d = d' — 1. Код Грэя является линейным кодом и представляется порождающей матрицей обычного двоичного кода с добавлением одной единицы в младшем разряде.
Ниже приводятся примеры образующих матриц без избыточных n-разрядных кодов, обеспечивающих в пределах апертуры ± й кодовое расстояние d [23].
* Метод апертурного контроля параметров в ТИ предложен Г. А. Майбородой.
Таким образом, предложенные без избыточные помехозащищенные коды позволяют повысить эффективность передачи коррелированных сообщений ТИ. По сложности реализации они близки к обычным корректирующим кодам. Эти коды являются подклассом более общего класса кодов, уменьшающих, а не только исключающих избыточность за счет апертурного контроля. Так, коды в примерах 3.7 и 3.8 могут быть дополнены общей проверкой на четность и дать d = 4 при одном избыточном разряде.


