Автоматическое противоаварийное управление - Алгоритмы адаптивной централизованной системы управления

Управляющие воздействия в адаптивной ЦСПА определяются непосредственным расчетом на УЭВМ в "реальном времени", т.е. в темпе процесса изменения стационарного режима. Расчет, как и в случае неадаптивного алгоритма, выполняется циклически с перебором всех расчетных аварийных возмущений, и для каждого из них определяются необходимые воздействия.
Очевидно, что цикл расчета на должен превышать интервала времени, в течение которого режим изменится настолько, что принятые решения окажутся непригодными к концу цикла. С учетом реальной интенсивности изменения стационарных режимов это время не должно превышать 1-2 мин. Казалось бы возникает противоречие между столь жесткими требованиями к вычислительным возможностям УЭВМ и высказанными ранее соображениями применительно к неадаптивной ЦСПА об огромном объеме вычислений на универсальных ЭВМ результаты которых закладываются в память УЭВМ. Принципиальное различие в алгоритмах неадаптивной и адаптивной ЦСПА состоит в том, что если в первом случае должны быть рассчитаны области устойчивости во всем реальном диапазоне изменения режимных параметров и вариантов исходной схемы, то во втором случае расчеты проводятся в единственной схеме и режиме, существующих в данный момент времени. При этом, строго говоря, даже не требуется определять пределы устойчивости, а лишь убедиться в обеспечении нормативных условий устойчивости в данном текущем режиме.
Однако, оценка устойчивости и выбор средств управления для ее обеспечения даже в одном режиме при нескольких десятках расчетных аварийных возмущений задача весьма непростая, учитывая жесткий лимит времени на выполнение всего цикла расчетов и ограниченные вычислительные возможности УЭВМ. Для преодоления этих трудностей разработаны специальные методика, алгоритмы и комплекс программ, базирующиеся на учете особенностей протекания переходных процессов в сложных энергосистемах.

В результате многочисленных исследований с использованием различных моделей и обобщения результатов анализа аварийных режимов в действующих энергосистемах показана принципиальная возможность все многообразие переходных процессов разделить (с позиций определения требований к управлению для обеспечения устойчивости) на две характерные группы.
К первой группе относятся процессы, определяемые аварийным отключением генераторной мощности иди элементов сети, при которых для того или иного "опасного сечения" не обеспечивается необходимый запас статической устойчивости в послеаварийном режиме или устойчивость простого перехода к этому режиму. При этом можно не учитывать собственные колебания отдельных электростанций, вызванные, например, сбросом мощности в результате глубокого снижения напряжения на шинах при коротком замыкании. Разумеется, что такое допущение предполагает сохранение динамической устойчивости этой электростанции, в частности и за счет противоаварийного управления.
Ко второй группе относятся процессы, связанные с ярко выраженной динамикой движения отдельных электростанций или узлов относительно остальной части энергосистемы. При возникновении опасности выпадения из синхронизма такой электростанции должны решаться локальные задачи сохранения устойчивости за счет использования соответствующих средств противоаварийного управления, желательно импульсного действия.
Такой подход позволяет разделить задачи управления, выделив для адаптивной ЦСПА задачи, связанные с обеспечением статической устойчивости и устойчивости простых переходов в сложных многосвязных энергосистемах. Оценка устойчивости в адаптивной ЦСПА выполняется с применением специальной методики. Динамические процессы второй группы при этом не учитываются, исходя из того, что они компенсируются локальными средствами управления. Другой прием, обеспечивающий сокращение времени вычислений, состоит в выделении двух различных циклов расчета - схемного и режимного. Причем в схемном цикле выполняются подготовительные расчеты, результаты которых не зависят или практически не зависят от режима энергосистемы, в основном это расчет различных эквивалентных схем, коэффициентов распределения, других вспомогательных величин. Эти расчеты лишь условно можно назвать циклическими, выполняются они по сигналу об изменении схемы энергосистемы. Остальные расчеты проводятся в режимном цикле с минимально возможным интервалом, определяемым длительностью перебора расчетных аварийных возмущений в текущем режиме.
Имея в виду высокие требования к надежности функционирования, необходимо обеспечить дееспособность ЦСПА вне зависимости от сбоев в измерении и передаче отдельных режимных параметров. Одним из наиболее действенных методов восполнения отказов отдельных датчиков и устройств телепередачи является применение так называемых программ оценивания состояния. Специальные методы расчета режима, используемые в этих программах, позволяют рассчитать с достаточной степенью точности режим, несмотря на отсутствие или неправильные показания отдельных входных величин. Для реализации такой возможности исходная информация, на основе которой проводится расчет режима, должна быть заведомо избыточной (обычно степень избыточности составляет 20-40%). Кроме того, с использованием программы оценивания состояния вычисляются параметры режима, непосредственное измерение которых не проводится, в частности -реактивные мощности. Собственно алгоритм дозировки управляющих воздействий, укрупненная блок-схема которого приведена на рис. 28, включает ряд программных блоков, базирующихся на специальных методических разработках. Далее кратко изложены методические основы наиболее важных из этих блоков.
Расчет послеаварийного режима в исходной базовой модели адаптивной ЦСПА осуществляется в линейной модели решением уравнений баланса активных мощностей. Значение послеаварийного перетока мощности каждого сетевого элемента определяется в виде суммы текущего значения перетока и его приращения, вызванного аварийным возмущением и управляющими воздействиями с учетом изменения частоты. Расчет проводится решением следующей системы уравнений:
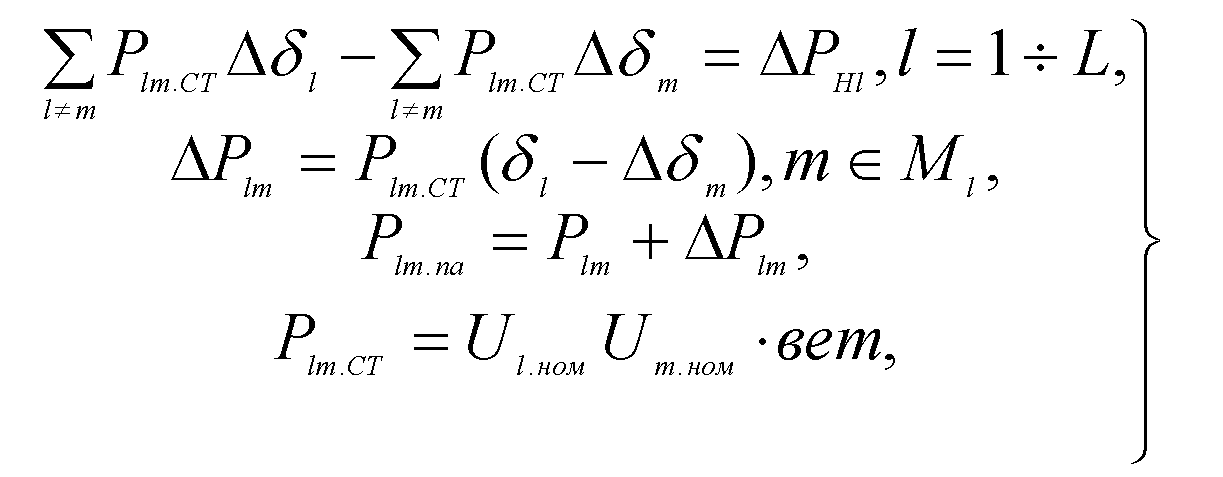(50)
где Δδ1, ΔδΜ - отклонения фаз напряжений в узлах l, m ; L - число узлов в системе; Ml - множество узлов, соединенных с узлом l с ветвями l-m ; вет - реактивная проводимость ветви l-m ; Ulном,Umном - номинальные значения напряжений в узлах lm ; Plmna , Plm.CT,Рlm - текущее значение мощности ветви между узлами l,m в исходном и послеаварийных режимах, максимальное значение этой мощности и изменение мощности при переходе к послеаварийному режиму; ΔΡΠ, ΔΡΗΙ - изменения генерации и потребления в узле l . Число линейной независимых первых уравнений в системе (50) составляет L - I.
Определение послеаварийного режима сводится к вычислению значений в узлах схемы и изменений потоков мощности в сетевых элементах схемы при найденных значениях ΔΡη — ΔΡΗΙ.
Правую часть первого уравнения (50) можно записать в виде: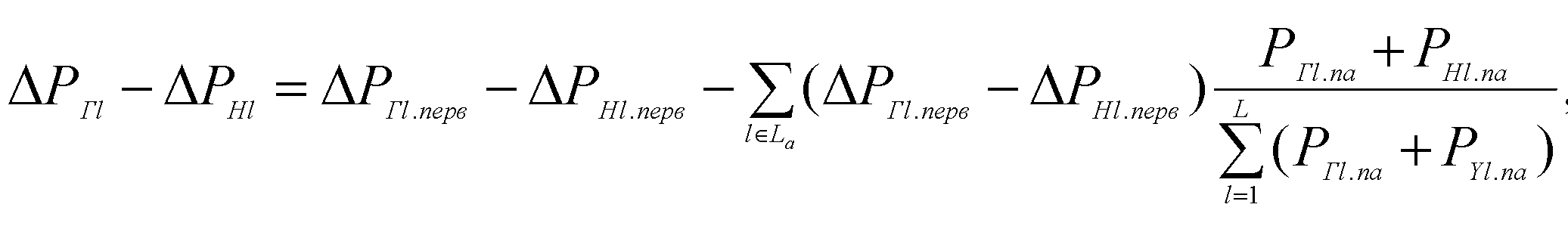

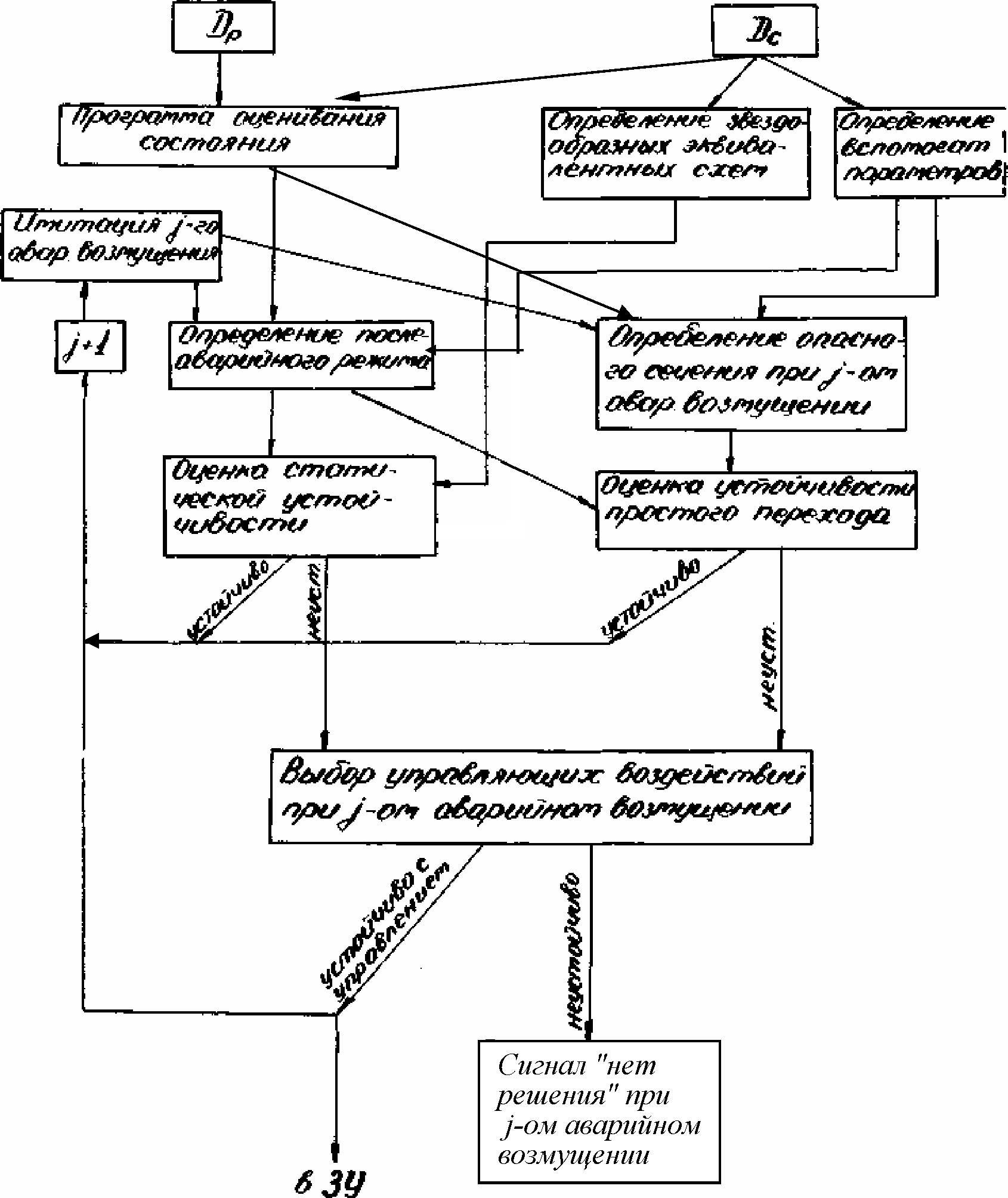
Рис. 28
где индексом "пера" обозначается первичное изменение генерации и нагрузки в узле, определяемые аварийным отключением и (или) управляющим воздействием; Pn na, PHl na - послеаварийные значения генерации и нагрузки в узле (без учета изменения частоты); La -множество узлов, в которых имеют место аварийные отключения или (и) управляющие воздействия.
Дополнительное уточнение послеаварийного режима получено при учете изменения потерь в послеаварийном режиме по отношению к исходному.
Оценка устойчивости в темпе процесса является наиболее сложной задачей адаптивной системы противоаварийного управления. Ниже излагаются основные положения метода быстродействующей оценки устойчивости базирующегося на идее узлового анализа устойчивости, который был ориентирован специально на применение в алгоритме ЦСПА.
На рис.29 в качестве примера приведена схема некоторой энергосистемы (а ) и одна из узловых моделей (для узла I) - б. Аналогичные модели строятся для всех остальных узлов. Как видно из приведенного рисунка, в узловой модели сохраняются непреобразованными генератор и нагрузка данного узла, а также все отходящие от него связи, за которыми подключается эквивалентные ЭДС. Эквивалентные ЭДС определяются из условия сохранения исходного режима в примыкающих к узлу элементах.

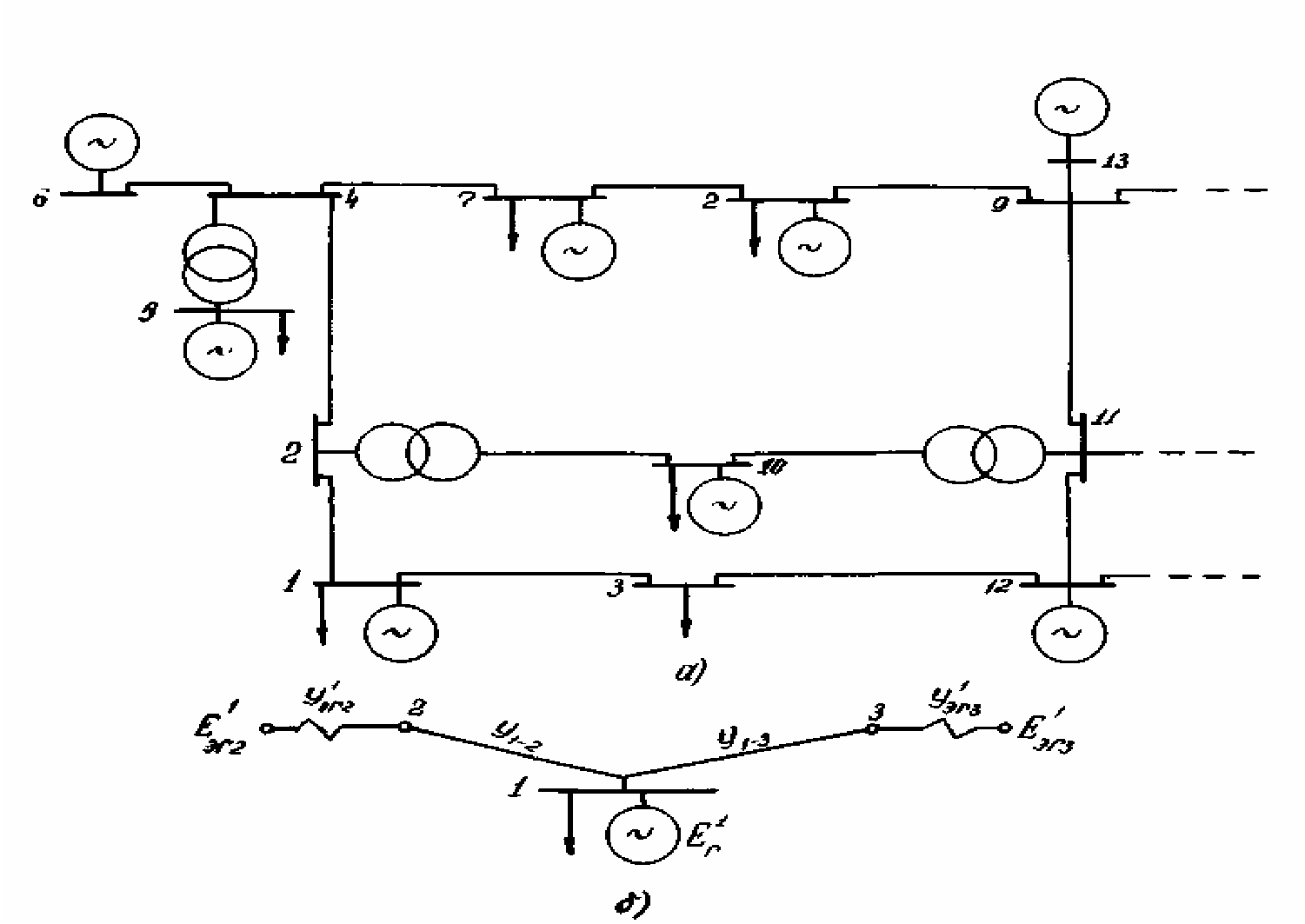
Рис. 29

Эквивалентные проводимости (Uэг) определяются из расчета режима растекания единичного тока от узла l при коротком замыкании всех ЭДС схемы. Пренебрегая активными сопротивлениями сетевых элементов, можно записать следующее соотношение для любой не преобразуемой ветви l-m , примыкающей к узлу l, в эквивалентной схеме:
(51)
Откуда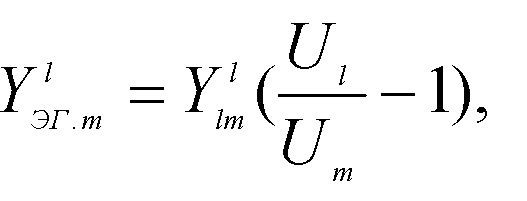
где Ul и Um - модули напряжения в узлах l,m, определяемые решением системы уравнений баланса токов в узлах исходной схемы:
YU = I (52)
при заданных (единичных) токах, т.е. являются элементами обратной матрицы Y-1. Последовательное решение (52) и (51) обеспечивает определение совокупности значений Ylэгm всех узлов моделей исходной схемы энергосистемы.
Эквивалентная ЭДС Ε1ЭГт в текущем режиме определяется по условиям
соответствия текущему значению напряжения центрального узла и активной и реактивной мощности не преобразуемого элемента l-m (реактивная мощность определяется на основе переработки исходной информации по программе оценивания состояния).
Эквивалентные ЗДС в послеаварийном (прогнозируемом) режиме (Ε 1ЭГтт )
тем же способом непосредственно определены быть не могут. Для их определения используется следующий прием.
В узловой модели узла l (рис. 30,а) каждый смежный узел представлен своей узловой моделью (рис. 30, б) с неизменными ЭДС, точки приложения которых как бы отодвинуты от узла l на один шаг по графу схемы относительно узловой модели рис. 30,а. Эквивалентную ЭДС смежного узла т при расчетах в узловой схеме рис. 30,а можно приближенно определить в зависимости от параметров узловой модели узла m (Пт ) и эквивалентных ЭДС лучей этого узла (Εтэг) определенных в текущем доаварийном режиме, и потоков активной мощности в этих узлах (Plmna), определенных по условиям послеаварийного режима: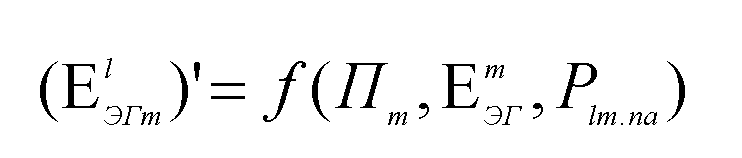

Рис. 30
Далее для получения уточненного значения ЭДС (ΕЭГт.па ) дополнительно в
тех же предпосылках определяются эквивалентные ЭДС в предаварийном режиме:

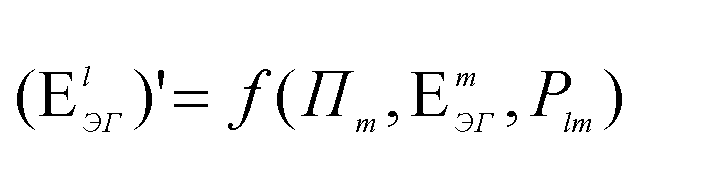
Наконец эквивалентные ЭДС в послеаварийном режиме определяются выражениями:
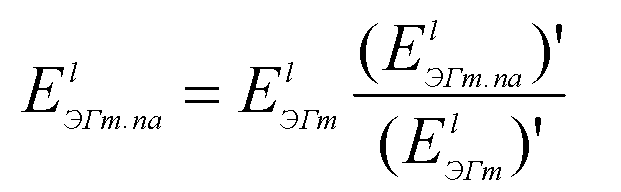(53).
Обратимся теперь к вопросу собственно оценки устойчивости в узловой модели.
В общем случае режим узловой модели задается значениями модулей эквивалентных ЭДС, в том числе и ЭДС генераторов центрального узла, активными мощностями генератора, нагрузки и лучей связи с внешней схемой, значением напряжения центрального узла U в исходном режиме и соответствующим ему значением реактивной мощности нагрузки QHl.
Устойчивость режима в узловой модели оценивается на основе анализа уравнений баланса активных и реактивных мощностей в узле, которые преобразуются к одному нелинейному уравнению баланса реактивных мощностей относительно напряжения центрального узла:
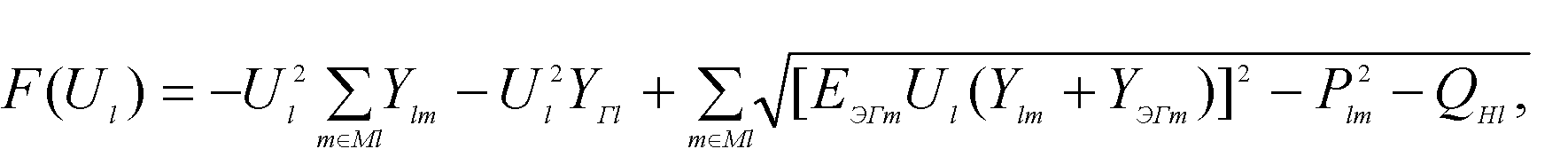(54)
где QHl - реактивная составляющая нагрузки узла l при задании ее PH = const, QH = const ( консервативная модель).
Один из критериев существования решения (54) очевиден: модуль напряжения U l не может быть комплексной величиной, и, следовательно, все подкоренные выражения (54) должны быть больше или равны нулю. Наибольшее из напряжений, соответствующих нулевым значениям подкоренных выражений, является критическим (Ul.kp). Положительный знак функции (54) при подстановке значения Ul = Ul kp является достаточным условием существования режима данной узловой модели.
В качестве достаточного условия не существования режима принята совокупность условий:
(55)
где ЕЭГп - эквивалентные ЭДС всех лучей звезды с центром l , включая и ЭДС генератора узла l, кроме ЕЭГт; Умн - взаимные проводимости между точкой приложения ЭДС ЕЭГ и точками приложения всех остальных ЭДС ЕЭГп звездообразной схемы с центром l.
Опыт расчетов показывает, что в подавляющем большинстве случаев два эти критерия позволяют выполнить разделение режимов на существующие и несуществующие, и лишь в остающихся редких случаях приходится прибегать к итеративному счету.
Приведенные решения направлены на обеспечение устойчивости энергосистемы в послеаварийных режимах, в которых предусматривается определенный запас статической устойчивости. Этот запас может быть при необходимости увеличен в расчете на динамику переходного режима. Но в некоторых случаях такой подход к учету динамики все-таки оказывается грубым, и тогда проводится дополнительная оценка динамической устойчивости на основе представления энергосистемы совокупностью "двухмашинных эквивалентов". При этом используются специальные алгоритмы выявления "опасных сечений" и оценки устойчивости простого перехода. Последняя основывается на применении критерия А. А. Горева или его модификаций, не требующих для оценки устойчивости итерационного счета.
Третьей важнейшей составляющей алгоритма является собственно выбор мест приложения и дозировка управляющих воздействий.
Процедура решения этой задачи может сводится к следующему.
Загрузка лучей звезды с центром в узле l характеризуется коэффициентами загрузки:
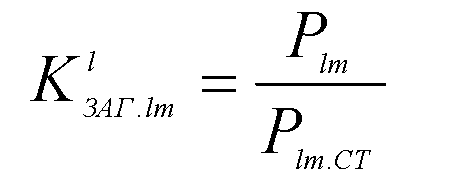(56)
Очевидно, что предельная поверхность в координатахв общем
случае вписана в единичный многомерный куб и приближается к сфере. Это позволяет в качестве близкой к оптимальной траектории перемещения изображающей точки за счет ввода управляющих воздействий принять перемещение по направлению, обратному радиус-вектору изображающей точки, а изменение величины радиуса-вектора - мерой приближения к предельной поверхности.
Так, например, при вводе управляющих воздействий в узлах ma, тб выражение для модуля радиуса-вектора точки, изображающей режим в звездообразной модели, может быть представлено в виде:
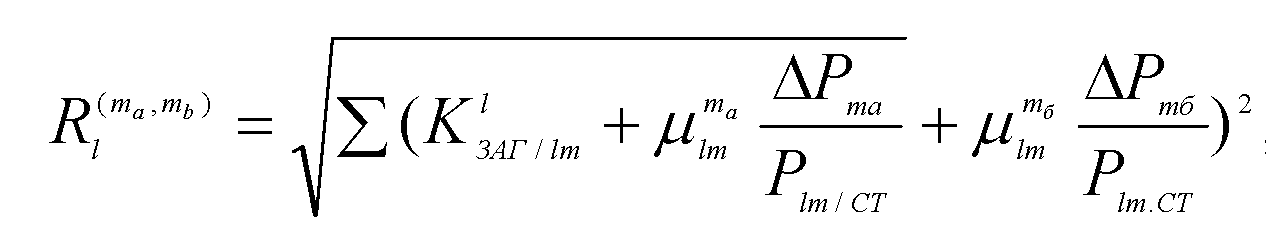, (57)
где ΔΡηα , АРтб - инекции от управляющих воздействий в узлах ma , тб, -коэффициенты распределения инекции в узлах та , тб на луч l-m.
Эффективность управляющего воздействия в узле та на изменение режима в звезде с центром l оценивается величиной проекции вектора изменения режима от управления на радиус-вектор изображающей точки послеаварийного режима без применения управляющих воздействий:
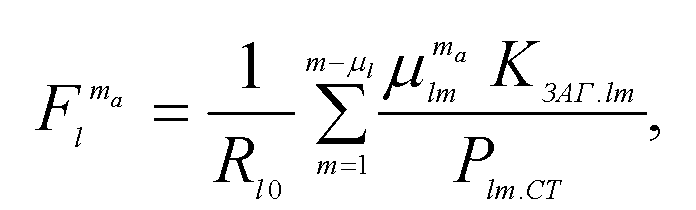(58)
где Rl0 - радиус-вектор в послеаварийном режиме без управления.
Для оценки эффективности управляющего воздействия в узле та по совокупности влияния на режим всех звезд используется следующая целевая
функция:
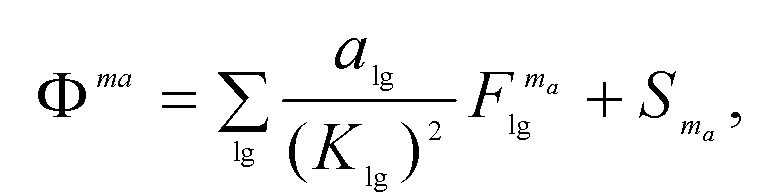(59)
где lgeLg - подмножество звезд, для которых выполняется
(60)
ξ - заданная положительная константа; Klg - коэффициент пропорциональности изменения режима всех лучей звезды lg по направлению вдоль радиуса-вектора режима без управления, при котором выполняется условие существования режима (54), причем
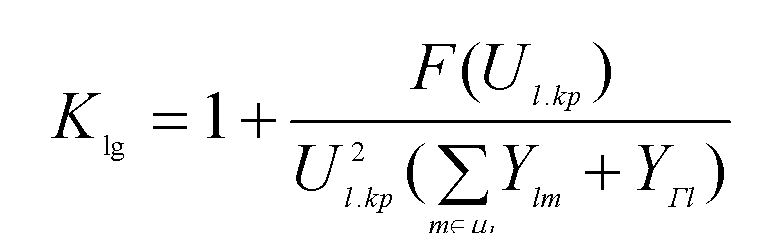(61)
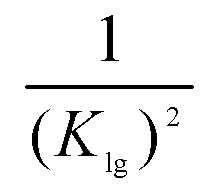- показатель тяжести режима в звезде; ag - дополнительный коэффициент (задаваемая константа), усиливающий показатель тяжести режима в звезде; Sma - штрафная функция для управления в узле mq по условиям некоторой звезды, не входящей на данном шаге выбора управляющих воздействий в подмножество Lg.
Подмножество Lg по условию (60) выбирается на основе компромисса между двумя противоречивыми требованиями. С одной стороны Lg должно быть достаточно полным, чтобы добиться управления, эффективного по условиям системы в целом. С другой стороны, чем шире Lg , тем больше объем вычислительной работы и соответственно - удлинение режимного цикла. В конечном счете решение этого вопроса, а также вопросов выбора перечисленных констант должно основываться на опыте расчетов.
Алгоритм ЦСПА претерпевает, как уже отмечалось, совершенствование с целью уточнения (исключения тех или иных допущений) по мере накопления опыта эксплуатации, использования более совершенной вычислительной техники и расширения объема используемой входной информации.