Экономика и управление качеством энергии - Математические методы оптимального управления качеством энергии

3. Математические методы оптимального управления качеством энергии*

Применительно к проблеме оптимизации качества электрической энергии наиболее подходящий критериальный показатель — минимум приведенных затрат. Но вместе с тем найдут применение модели, целевые функции которых представляют собой некоторые параметры режима, а ограничения — нормативные требования качества электроэнергии, допустимые расходы ресурсов, пропускные способности элементов системы электроснабжения, а также любые другие требования более высокого ранга, которым следует отдать приоритет.
Перечислим наиболее характерные соотношения, используемые как целевые функции в задачах оптимизации качества электроэнергии (для детерминистских моделей непосредственно для стохастических и смешанных — в виде вероятности, плотности вероятности, математического ожидания, дисперсии или других моментов соответствующих распределений): 1) расчетные затраты или их составляющие; 2) показатели качества электроэнергии; 3) потери активной мощности в элементах систем электроснабжения; 4) наиболее важные параметры режима; 5)         действительная реактивная мощность основной частоты, зависящая от установленной мощности; 6) показатели надежности оптимизирующих устройств и т. д.
Отметим некоторые соотношения, которые могут выступать в виде ограничений моделей оптимизации качества электроэнергии, причем сохраним в силе приведенное выше замечание о возможности их вероятностной интерпретации: 1) пороговые значения отдельных показателей качества электроэнергии или совместных по ряду показателей; 2) расходы ресурсов в широком смысле слова; 3) пороговые значения наиболее важных параметров режима; 4) балансы мощностей; 5) недопустимость перегрузки оптимизирующих устройств и элементов системы электроснабжения; 6) условия резонансной настройки контуров;

1. условия, исключающие нежелательные резонансные явления в системе, которые связаны с включением оптимизирующих устройств; 8) пороговые значения показателей надежности оптимизирующих устройств; 9) условия, обеспечивающие необходимое качество переходных процессов в оптимизирующих устройствах; 10 пороговые значения устойчивости узлов нагрузки и т. д.

В зависимости от структуры системы электроснабжения в задачах оптимизации качества электроэнергии можно комбинировать различные сочетания приведенных выше целевых функций и ограничений, и лишь требование адекватности реальной действительности остается неизменным при конструировании математических моделей. На практике нередко возникает необходимость улучшения качества электроэнергии по одному показателю, но чаще по нескольким одновременно. В соответствии с этим различают задачи локальной и многоцелевой (комплексной) оптимизации.*

* Применение многоцелевой оптимизации к задачам энергетики показано в [64].

структуры (Qycт); 7) характеристики надежности (Н) системы электроснабжения и ее элементов; 8) характеристики устойчивости (kзап) узлов нагрузки; 9) характеристики качества переходных процессов в элементах системы.
Перечислим возможные ограничения: 1) пороговые (допустимые) значения напряжения обратной последовательности в узлах системы; 2) пороговые значения тока обратной последовательности в ветвях системы; 3) допустимый диапазон значений напряжения прямой последовательности в близлежащих узлах системы (U1); 4) допустимые расходы ресурсов; 5) местные балансы реактивной мощности (Qбал); 6) пропускные способности элементов системы; 7) пороговые значения запаса устойчивости углов нагрузки; 8) пороговые значения показателей надежности оптимизационной структуры и т. д.
В табл. 18 приведены некоторые модели симметрирования режимов, записанные в символической форме. Особенность этих моделей состоит в том, что в них режимные параметры целевых функций и ограничений представляются квадратичными функциями. С позиций математического программирования такие модели интерпретируются как общие нелинейные модели, а задача симметрирования режима на их основе — как общая нелинейная экстремальная задача.
Общие нелинейные модели, наиболее полно отражающие процесс симметрирования режимов, требуют для своего построения сложных алгоритмов математического программирования. Поэтому актуальным является любое упрощение моделей, способное сохранить их адекватность реальной действительности. В качестве таких упрощений могут применяться методы линейного и квадратичного программирования.

Продолжение табл. 18

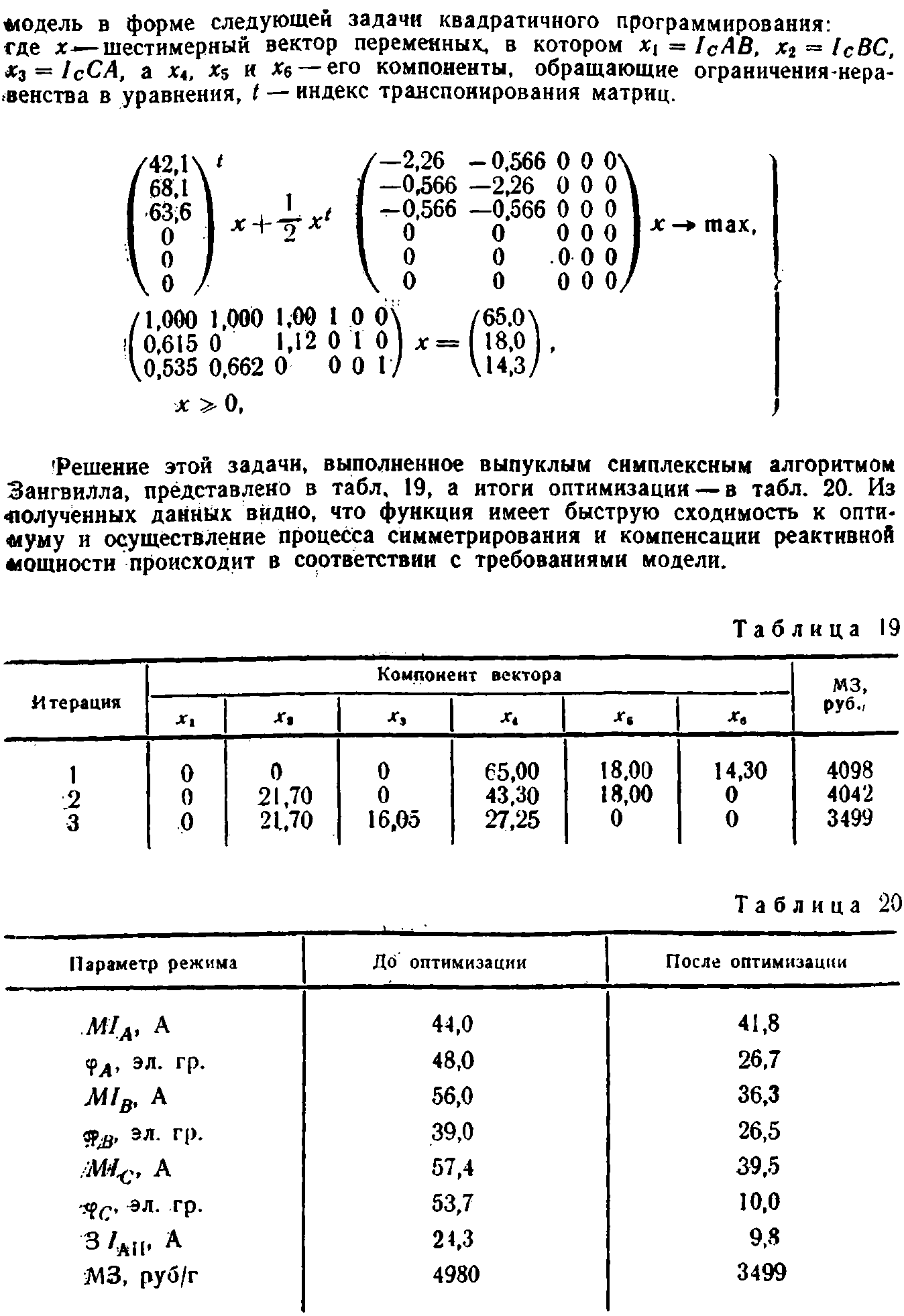
Для разработанных математических моделей оптимизации качества электроэнергии к настоящему времени опробовано в практическом решении достаточно большое число алгоритмов. Некоторые из них относятся к методам штрафных функций, в

Схема 5. Анализ линейных моделей.

 

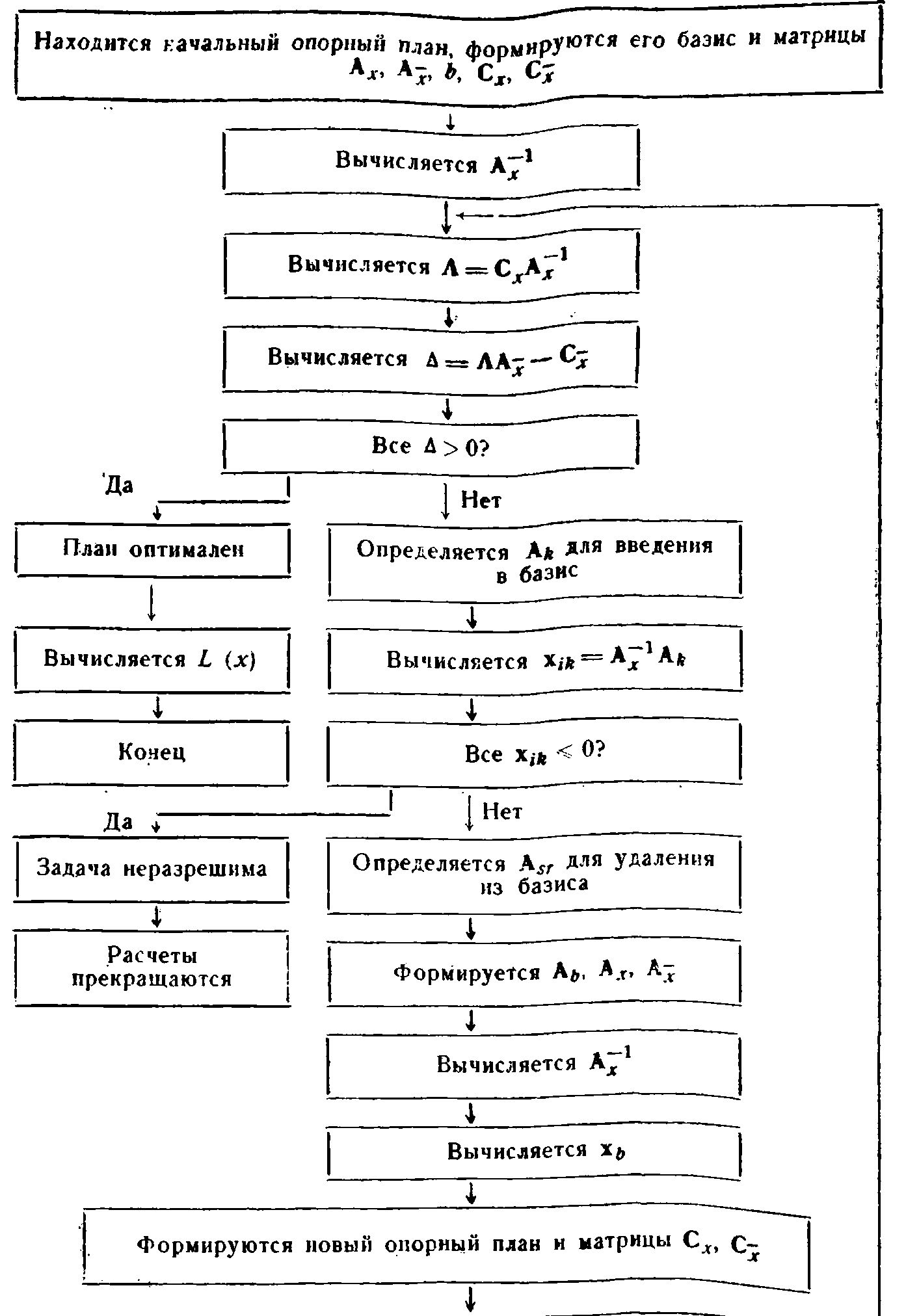
Рассмотрение некоторых алгоритмов математического программирования позволяет сделать следующие выводы:

1. для анализа общих нелинейных моделей оптимизации качества электроэнергии наиболее предпочтительным является метод комбинированных внутренне-внешних штрафных функций с использованием алгоритмов безусловной оптимизации, идентифицирующих оптимальную точку на основе условий второго порядка;
2. для анализа нелинейных моделей оптимизации качества электроэнергии с линейными ограничениями эффективным является алгоритм Франка и Вулфа непосредственной линейной аппроксимации;
3. для анализа моделей оптимизации качества электроэнергии, вписывающихся в схему квадратичного программирования, наиболее целесообразным является выпуклый симплекс-алгоритм Зангвилла;
4. для анализа моделей оптимизации качества электроэнергии, вписывающихся в схему линейного программирования, могут быть использованы любые варианты конечных и итеративных методов, в том числе алгоритм обратной матрицы Канторовича.