В практической деятельности предприятия часто возникают ситуации, когда необходимо выполнение большого числа однородных требований. При этом под понятием «требование» понимается запрос на удовлетворение какой-либо потребности, например необходимость исправления вышедшего из строя оборудования, устройства, спрос на определенную продукцию и т. п. Под выполнением или обслуживанием понимается процесс удовлетворения этой потребности.
По своей природе обслуживание может иметь самый различный характер. При этом каждое поступившее требование нуждается в обслуживании со стороны какого- либо устройства, человека или группы людей. Все средства, которые осуществляют обслуживание, называются обслуживающими аппаратами или обслуживающими устройствами. На практике, как правило, приходится иметь дело не с одним обслуживающим аппаратом, а с ограниченной группой аппаратов. Совокупность однородных обслуживающих аппаратов называется обслуживающей системой. При этом под однородными аппаратами понимаются такие, которые способны удовлетворять одинаковые требования.
В том случае, когда число обслуживающих аппаратов в обслуживающей системе ограничено, возможна ситуация, при которой число обслуживающих аппаратов будет меньше, чем количество требований, поступающих на обслуживание. В этом случае образуется очередь, длина которой определяется количеством требований, находящихся в ней.
Одним из основных требований эффективной работы обслуживающей системы является максимальное удовлетворение запросов на обслуживание в течение заданного промежутка времени (или обеспечение минимальных затрат по функционированию системы). Определение наилучших параметров таких систем обслуживания является предметом теории массового обслуживания
Рассмотренная выше общая схема обслуживания является характерной для организации ремонтов энергетического оборудования на предприятии. В этих условиях методы теории массового обслуживания могут найти широкое применение при определении рациональной численности ремонтного персонала, ремонтных баз и оборудования.
Процесс массового обслуживания протекает по следующему принципу: требования на обслуживание поступают в обслуживающую систему, обрабатываются обслуживающим аппаратами и покидают ее. Для обеспечения успешной работы обслуживающей системы используются методы количественных расчетов, которые позволяют обоснованно судить о том, является ли данный способ организации лучше или хуже другого, справляется ли данный вариант обслуживающей системы с работой по обслуживанию лучше других вариантов или нет, и т. д.
Все задачи массового обслуживания имеют вполне определенную структуру, которая схематически показана на рис. 8-1. Последовательность поступления требований на обслуживание называется потоком. Поток требований, нуждающихся в обслуживании и поступающих в обслуживающую систему, называется входящим потоком, а покидающих обслуживающую систему — выходящим потоком.
Остановимся на одной из типичных систем массового обслуживания — системе с ограниченным потоком требований, когда время ожидания начала обслуживания не ограничено, а требование, попавшее в систему обслуживания, будет находиться в ней, пока обслуживание не завершено.
Пусть рассматриваемая обслуживающая система состоит из конечного числа обслуживающих аппаратов.
причем каждый аппарат системы, может одновременно обслужить только одно требование. В момент поступления очередного требования возможны два случая; либо в это время имеются свободные аппараты, либо все аппараты заняты. Если есть свободные аппараты, то один из них немедленно приступает к обслуживанию поступившего очередного требования, если же все аппараты заняты, то требование ждет, пока освободится один из обслуживающих аппаратов. Очевидно, что если число требований, нуждающихся в обслуживании, превысит число обслуживающих аппаратов, то образуется очередь.
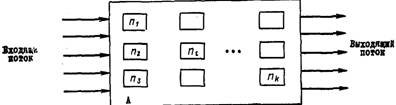
Рис. 8-1. Схематическое изображение системы массового обслуживания.
я,, л2 nh — обслуживающие аппараты; А — обслуживающая система.
Предположим, что время обслуживания есть случайная величина v, подчиненная показательному закону распределения
![]() (8-1)
(8-1)
где P[v<i} — вероятность того, что время обслуживания меньше некоторой заданной величины /.
Поток поступающих требований ограничен, т. е. одновременно в системе обслуживания не может находиться более m требований, где т — конечное число. При этом часть времени они находятся в системе обслуживания, а часть вне ее, т. е. в очереди.
Поток требований обладает следующими двумя свойствами :
во-первых, вероятность того, что требование поступит на обслуживание за время (t, если оно не посту-
пило до момента t, равна XAt-\-0(t), где А,>0 и не зависит от т, t и числа требований, поступивших до него;
во-вторых, моменты поступления данного требования в пересекающиеся промежутки времени — независимые события.
При этом, если требование не поступило до момента о, вероятность его непоступления до момента ta~\~t равна:
![]() (8-2)
(8-2)
где к—частота возвращения требования в обслуживающую систему.
С увеличением X возрастает вероятность поступления (или возвращения) требования в обслуживающую систему. Промежуток времени, в течение которого обслуживаемый объект не требует обслуживания, подчинен показательному закону. Это означает, что среднее время нахождения его вне системы обслуживания равно 1/А,.
В качестве критериев, которые характеризуют качество функционирования рассматриваемой системы, принимаются следующие:
отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе.
Это отношение можно назвать коэффициентом простоя обслуживаемого объекта-,
отношение среднего числа незанятых обслуживающих аппаратов к их общему числу. Это отношение есть коэффициент простоя обслуживающего аппарата.
Первый критерий характеризует потери времени за счет ожидания начала обслуживания. Второй критерий показывает полноту загрузки обслуживающей системы. Представляют интерес и такие критерии, как средняя длина очереди, вероятность иметь в очереди больше, чем заданное, число требований и т. д. Для оценки экономичности ремонта важен не каждый из критериев, а оптимальное соотношение их по приведенным затратам.
Обслуживающая система может находиться только в т+1 состоянии, так как в ней не может одновременно находиться больше m требований. При п обслуживающих аппаратах очередь возникает лишь тогда, когда число аппаратов п<т
Обслуживающая система может находиться в п-\-1 состоянии: все обслуживающие аппараты свободны, т. е. ни один не занят; занят один обслуживающий аппарат; заняты два обслуживающих аппарата и т. д.; заняты все га обслуживающих аппаратов. Обозначим через N (t) число аппаратов, занятых в момент времени t при условии, что в начальный момент занято k аппаратов. Функция N(t) —случайная величина, которая определяется: моментами освобождения тех k аппаратов, которые были заняты в начальный момент, моментами поступления новых требований на обслуживание, моментами окончания обслуживания этих новых требований. Если в некоторый момент времени занят k{ аппарат, т. е. N(ti)=ku то дальнейшее течение процесса обслуживания не зависит от того, что было до момента tx. Моменты появления новых требований не зависят от того, что было до момента 11, так как поток требований простейший, и, следовательно, обладает свойством отсутствия последействия.
Рассмотрим ремонт энергооборудования как систему массового обслуживания. Под требованием можно понимать различные неисправности, поломки оборудования, а под обслуживанием — устранение этих неисправностей, т. е. ремонт оборудования. Ремонтную бригаду можно рассматривать как обслуживающую систему, а ремонтных рабочих как ее составляющие (обслуживающий аппарат).
Во время рабочей смены может случиться, что вышедшее из строя оборудование некому будет ремонтировать, так как все ремонтные рабочие будут заняты ремонтом оборудования, ранее вышедшего из строя. В таком случае оно будет ждать начала обслуживания до тех пор, пока освободится кто-либо из ремонтных рабочих. Если неисправного оборудования оказывается больше наличия свободных ремонтных рабочих, то образуется очередь. В нашем примере входящим потоком в обслуживающую систему будут требования на устранение различных поломок и неисправностей в оборудовании; выходящим потоком — исправное оборудование.
Применение теории массового обслуживания рассмотрим на примере ремонта электрооборудования металлорежущих станков в цехе машиностроительного завода.
Функционирование ремонтной службы цеха происходит следующим образом. В главном проходе цеха находится доска требований, на которую заносится номер станка, имеющего мелкую поломку или аварию. Через некоторое время к доске подходит свободный ремонтный рабочий и идет обслуживать данный станок. За исключением очень редких случаев требования обслуживаются в порядке их поступления.
В течение 30 дней проводились наблюдения за поступлением и обслуживанием требований. Появление записи на доске считалось началом поступления требования; когда ремонтный рабочий стирал номер, то этот момент принимался за окончание обслуживания. Время нахождения требования на доске считалось временем простоя станка. Наблюдения велись по схеме, приведенной в табл. 8-1.
Таблица 8-1
Схема выборочного обследования аварийности электрооборудования механического цеха

Из схемы видно, что наблюдения велись по два часа в день по скользящему графику. Кроме того, были проведены контрольные наблюдения по 4, 3 и 7 ч соответственно на 13, 14 и 15- и (28, 29 и 30 ) день наблюдений. В выборочное обследование были включены наиболее характерные моменты производственной деятельности цеха: начало, середина и конец рабочего дня, рабочей недели, месяца, предпраздничные и послепраздничные дни. Результаты наблюдений фиксировались через каждые 10 мин.
После 10 дней наблюдений (по 2 ч в день) была проведена первоначальная обработка результатов с целью оценки репрезентативного числа наблюдений.
Так как каждое наблюдение проводилось по 2 ч, то всего при заданной точности расчетов требуется 56 ч наблюдений. Наблюдения проводились 76 ч, что вполне достаточно для получения достоверных результатов. Число станков в цехе — 480. Ремонтная бригада состоит из 9 человек. Требование, поступившее в систему обслуживания (т. е. неисправность электрооборудования на каком-либо станке), может покинуть ее только тогда, когда оно полностью устранено. Требований, ожидающих обслуживание, может накопиться довольно много. В таком случае совокупность требований образует очередь. Требования обслуживаются в порядке их поступления. Рассматриваемая система обслуживания является системой с ожиданием или системой без потерь.
На основании проведенных наблюдений построена характеристика потока требований. В 10-минутный интервал либо не поступало ни одного требования, либо поступало только одно требование. В результате обработки этих наблюдений была составлена таблица частот и распределения вероятностей поступления требований на ремонтное обслуживание (табл. 8-2).
Частота и распределение вероятностей поступления требований на ремонтное обслуживание
Число требований k | Частота наступления событий г | Эмпирическая вероятность Р*? |
0 | 203 | 0,445 |
1 | 163 | 0,357 |
2 | 67 | 0,147 |
3 | 19 | 0,042 |
4 | 4 | 0,009 |
Более 4 | — | 0,000 |
Всего | 456 | 1,000 |
Критериями, характеризующими качество функционирования рассматриваемой системы, были выбраны: средняя длина очереди (8-7); коэффициент простоя оборудования в ожидании ремонта (8-8); среднее число требований, находящихся в обслуживающей системе (8-9); среднее число свободных обслуживающих аппаратов (8-10); коэффициент простоя обслуживающего аппарата (8-11).
Все эти критерии непосредственно зависят от Рь, где Ph — вероятность того, что в системе на обслуживании находится k требований. Следовательно, прежде чем провести оценку критериев, необходимо определить значения вероятностей Ph.
Для непосредственного вычисления вероятностей того, что в системе находится ровно k требований, воспользуемся формулами (8-4) и (8-5).
По формуле (8-4) определяется вероятность того, что в системе находится k требований, когда число требований не превосходит числа ремонтных рабочих п. В противном случае используется формула (8-5).
Рассмотрим эти две формулы. Очевидно, что т, п и k — известные величины. Величину Р0 можно определить из выражения (8-6). Тогда для определения значения Ph необходимо найти отношение A./V. Имея это отношение, можно решить задачу определения оптимального числа ремонтных рабочих, необходимых для аварийного ремонта электрооборудования на станках механического цеха.
Выше величина %* была определена, как среднее число остановов станков в час, или как частота возвращения требования в системе (Л* = 4,868 остановов/ч).
Определим v, где 1/v — среднее время нахождения требования в системе. Для этого составим таблицу, в которой принимаются во внимание только требования, поступившие и обслуженные в период наблюдения (табл. 8-4); всего таких требований 325.
Как видно из табл. 8-4, чаще всего требование находилось в системе около 60 мин.
Таблица 8-4
Зависимость частот поступления требований от времени] ”] нахождения их в системе обслуживания
Время нахождения требования в системе t, мин | Частота поступления требований г | Время нахождения требования в системе t, мин | Частота поступления требований г |
10 | 0 | 70 | 56 |
20 | 3 | 80 | 28 |
30 | 12 | 90 | 10 |
40 | 33 | 100 | 6 |
50 | 62 | 110 | 4 |
60 | 108 | 120 | 4 |
|
| Свыше 120 | — |
|
| Всего | 325 |
т
Определение поправочного коэффициента
Див наблюдения | Число требований, находящихся в системе | Число фактически поступивших требований |
1 | 44 | 49 |
2 | 38 | 41 |
3 | 35 | 40 |
Ито го | 117 | 130 |
Это означает, что в среднем каждый станок в течение 100 ч работы останавливается из-за поломок и аварий электрооборудования 1,122 раза, т. е. время между остановами станка равно приблизительно 90 рабочих часов.
Определим отношение A/v=0,0122-1,017=0,0114.
Далее воспользуемся формулами (8-4) и (8-5) для определения вероятностей Рк и основных критериев эффективности ремонтного обслуживания (табл. 8-6).
Таблица 8-6
Характеристика критериев эффективности системы ремонтного обслуживания
Число ремонтных рабочих л | Среднее число станков, стоящих в очереди М, | Среднее число ремонтируемых и ожидающих ремонта станков Mi | Среднее число свободных ремонтных рабочих Ms | Процент загрузки ремонт- даго рабочего | Процент простоя станка в ожидания начала обслуживания | Коэф- |
6 | 5,08233 | 10,44351 | 0,64887 | 89,32 | 1,059 | 0,02176 |
7 | 1,34244 | 6,73172 | 1,60788 | 77,03 | 0,279 | 0,01403 |
8 | 0,46156 | 5,86180 | 2,59892 | 67,51 | 0,096 | 0,01221 |
9 | 0,17043 | 5,57393 | 3,59622 | 60,04 | 0,035 | 0,01161 |
10 | 0,06326 | 5,46801 | 4,59524 | 54,05 | 0,012 | 0,01139 |
И | 0,02311 | 5,42817 | 5,59390 | 49,14 | 0,005 | 0,01131 |
12 | 0,00828 | 5,41363 | 6,59338 | 45,05 | 0,002 | 0,01128 |
13 | 0,00269 | 5,40622 | 7,59380 | 41,60 | 0,0006 | 0,01127 |
14 | 0,00081 | 5,40671 | 8,59375 | 38,62 | 0,00016 | 0,01126 |
Приведенные затраты для некоторых металлорежущих станков
Тип станка | Марка | Коэффициент производительности Я | Приведенные затраты Z, коп. | Количеств) шт. |
Токарный | 1А62 | 1 | 111,5 | 20 |
Токарный | 162 | 1,3 | 94,8 | 200 |
Револьверный | 1336М | 2,2 | 46,6 | 8 |
Токарно-револьверный | 123 | 5 | 32,4 | 2 |
автомат |
|
|
|
|
Токарно-многорезцовый | 1720 | 2 | 62,1 | 30 |
То же | 1730 | 2 | 71,0 | 10 |
Вертикально-фрезерный | 6Б12 | 1 | 122,8 | 14 |
То же | 6Н12 | 1 | 130,2 | 10 |
То же | 6Н13П | 1 | 145,7 | 10 |
То же | 6Н12П | 1 | 142,2 | 12 |
Протяжной | 7А510 |
| 35,3 | 6 |
Зубофрезерный | 532 | 1 | 100,6 | 15 |
Зубодолбежный | 5А12 |
| 81,0 | 10 |
Зубострогальный | 526 | 1 | 103,1 | 2 |
Зубоше винтовальный | 5714 |
| 42,4 | 4 |
Зубозакругляющий | 5680 | 1,5 | 65,4 | 4 |
Шлицефрезерный | 5617 |
| 22,3 | 8 |
Вертикально-сверлильный | 2125 | 1 | 87,6 | 6 |
То же | 2П150 | 1 | 112,8 | 4 |
Настольно-сверлильный | 2А106 | 1 | 81,4 | 2 |
Крупношлифовальный | 3151 |
| 134,7 | 11 |
Крупношлифовальный | ЗГ12М | 1 | 133,9 | 10 |
Бесцентрошлифовальный | 3180 | 3 | 53,7 | 2 |
Прочие | —• | — | — | 80 |
Итого | — | 1 |
| 480 |


