Линии электропередачи 345 кВ и выше - Данные для расчета акустического шума от ВЛ

1. ДАННЫЕ ДЛЯ РАСЧЕТА АКУСТИЧЕСКОГО ШУМА ОТ ВЛ

Ниже дано описание порядка расчета акустического шума от ВЛ. В дополнение приводятся таблицы для непосредственной оценки уровня шума без каких-либо вычислений.
Вычисление уровней случайного акустического шума. Ниже приводится последовательность оценки случайного шума, определенного с помощью фильтра N.

1. Оценивается максимальная напряженность для каждой фазы. Максимальная напряженность отдельного провода фазы определяется как среднеквадратичное значение максимальной напряженности проводов фазы. Обычно отдельные провода «нормального» пучка имеют максимальные напряженности, которые мало отличаются друг от друга. Среднее из максимальных напряженностей проводов принимается за максимальное значение напряженности Ешах фазы.
2. Акустическую мощность А', создаваемую при сильном дожде, можно найти из рис. 4.5.23 или вычислить по уравнению (4.5.3). Полученные значения относятся к одному проводу диаметром 3,8 см.
3. Акустическая мощность А, генерируемая фазой, вычисляется для необходимого количества проводов и принятых диаметров проводов с помощью уравнения (4.5.2).
4. На некотором расстоянии от ВЛ для одной фазы оценивается /г по уравнению (4.2.4), в котором h— 1 (не учитывается отражение от земли). Для учета затухания звука в воздухе результат умножается нагде a≈0,0075 м-1 (см. § 4.2), a R — расстояние между микрофоном и проводом.
5. Акустическая мощность всех фаз суммируется алгебраически.
6. Вычисляется уровень звукового давления по уравнению (4.2.7).
7. Находится уровень звукового давления, дБ (А), с помощью уравнения (4.6.1) при сильном дожде:

где р — уровень звукового давления, Н/м2.

1. Акустический шум для «мокрого провода» (при тумане, слабом дожде или сразу после дождя) определяется таким же способом. Однако до вычислений по п. 5 акустическая энергия, определяемая по/ п. 4 для условий «сильного дождя», пересчитывается для условий «мокрого провода» в соответствии с рис. 4.5.25, 4.5.26 или с помощью уравнений (4.5.4) — (4.5.6).
2. Для фаз, конструкция которых оптимизирована (асимметричная конфигурация — вариант на рис. 4.5.36,а), вначале вычисляется акустический шум для «мокрого провода», как это сказано выше, применительно к «нормальному» пучку. Затем делается корректировка на акустическую энергию каждой фазы в соответствии с рис. 4.5.35 с увеличением напряженности приблизительно на 5% по сравнению с рассчитанным в п. 1.

Акустическая энергия при «сильном дожде» для фазы оптимальной конструкции на 20—60% (1—2 дБ) больше, чем энергия правильного пучка.
Ниже приводится числовой пример.
Определяется шум на расстоянии 15 м от крайней фазы ВЛ 1145 кВ со следующими размерами: фаза D=100 см состоит из восьми проводов, d=4 см, расстояние между фазами 18,5 м, средняя высота над землей 22 м, на высоте 35 м подвешены два грозозащитных троса (d—2,5 см), расстояние между тросами 30,5 м.
Вычисляются максимальные напряженности: для средней фазы 14,53 кВ/см, для крайней 13,64 кВ/см.
Генерируемая акустическая мощность А' для провода (d=3,8 см) по рис. 4.5.23 определяется следующим образом, дБ сверх 1 мкВт/м: для средней фазы

для крайней фазы

для п=8 и d=4 см

что дает для средней фазы Л=93 мкВт/м, для крайней фазы Л=43 мкВт/м.
До точки, находящейся на расстоянии 15 м от крайней фазы по горизонтали с учетом высоты над землей, находим:
для крайней фазы

для средней фазы

для дальней фазы

Акустическая мощность на расстоянии 15 м от крайней фазы оценивается по уравнению (4.2.4), преобразованному для учета затухания, мкВт/м2:

Среднеквадратическое значение критической напряженности Eс, при которой уровень звукового давления для «мокрого провода» на 6 дБ меньше, чем таковой при сильном дожде [см. уравнение (4.5.5) или рис. 4.5.25]: Eс=14 кВ/см.
Поправка С к энергии в соответствии с уравнением (4.5.6) или рис. 4.5.26:
для средней фазы

для крайней фазы

Соответственно мощности становятся равными, мкВт/м2:
Повторяя расчеты по пп. 5—7, для новых величин / получим:

Подобным образом можно определить профиль акустического шума (рис. 4.6.1).
Для оптимизированной конструкции фазы, диаметр которой сохраняется (D=100 см), шум уменьшается.
Поправка С' определяется по рис. 4.5.35 для напряженностей на 5% больших, чем получены в п. 1, т. е.:
14,53*1,05=15,25 кВ/см и 13,64-1,05=14,35 кВ/см при d— 4 см.
Для средней фазы уменьшение шума равно 11 дБ (поправка E72=0,08), для крайней уменьшение шума больше 12 дБ (поправка С'\—^2=0,062), следовательно, /1=0,06^<0,004; /2=0,15^2=0,012; /3=0,02С'3<0,002;
мкВт/м2=0,017* 10-6 Вт/м2; р= =20 ]/7 =0,0027 Н/м2=42,5 дБ (А).
Влияние опор, провисания проводов) и грозозащитных тросов. Выше не учитывались влияние опор и провисания проводов. На рис. 4.6.2 показаны влияние опор и провисания проводов на напряженность Е (Еср — среднее значение напряженности в пролете). Как видно, напряженность поля на поверхности провода изменяется очень мало. К тому же провисание влияет на шум у земли под ВЛ в направлении от середины пролета к опоре из-за разницы расстояний от провода до земли (рис. 4.6.3).

Рис. 4.6.1. Пример горизонтального профиля акустического шума.
1 — при «сильном дожде»; 2 — при «мокром проводе».

Грозозащитные тросы также мало влияют на общий шум от ВЛ. Это обусловлено их небольшими размерами,

Рис. 4.6.2. Влияние спор (/) и высоты подвески провода над землей (2) на напряженность поля на средней фазе ВЛ 500 кВ.
Рис. 4.6.3. Изменение акустического шума по длине пролета по сравнению с идеальной линией без учета влияния опор на акустический шум при неизменной высоте подвески проводов.
1 — мощность по отношению к измерению на уровне земли; 2 — шум.
малым числом (по отношению к общему количеству проводов) и большой высотой над землей.
Тем не менее желательно, чтобы грозозащитные тросы имели напряженность меньше, чем напряженность, соответствующая видимой короне. При соблюдении этих

условий грозозащитные тросы не будут увеличивать акустический шум и радиопомехи от ВЛ.
Расчет уровня акустического шума — «шипения». Результаты, представленные в § 4.5, позволяют определить уровень звукового давления при частоте 120 Гц для «нормального» пучка проводов при сильном дожде.
Ниже приводится последовательность расчета.

1. Оценивается максимальная напряженность Етах для каждой фазы.
2. Находится акустическая мощность по рис. 4.5.27 или уравнению (4.5.8).
3. Вводится поправка на диаметр провода в фазе в соответствии с рис. 4.5.29 или уравнением (4.5.10).
4. Вводится поправка на число проводов в фазе в соответствии с рис. 4.5.29 или уравнением (4.5.10).
5. Звуковое давление в дБ преобразуется в Вт/м.

1. Определяются уровни звукового давления   прямой и отраженной волны для каждой фазы i. При этом используется уравнение (4.5.7), преобразованное для 3-фазной линии следующим образом:

(4.6.1)
где индексы d и г соответствуют прямой и обратной волнам; фг — фазовый угол для напряжения в фазе i\ Ri,r — расстояние между зеркальным изображением фазы и точкой измерения; Ritd — расстояние между фазой i и точкой измерения; k — коэффициент отражения, значение которого при 120 Гц в практических случаях равно приблизительно единице; X—длина звуковой волны (при /=120 Гц А=2,85 м).

1. Добавляется волновое давление с учетом его значения и фазы.
2. Для погодных условий, отличных от сильного дождя, при небольшом количестве данных можно сделать попытку определения уровня давления, если известны потери на корону. Используется корреляция между потерями на корону и уровнем давления при 120 Гц для каждой фазы.

Используя данные, вычисленные по пп. 1—7, можно определить горизонтальный профиль уровня давления при «шипении». Пример расчета приведен на рис. 4.6.4, на котором показаны зависимости при разной высоте точки измерения. Результаты сильно зависят от расстояния от точки измерения до земли и горизонтального расстояния, поскольку в некоторых сочетаниях звуковое давление складывается, тогда как в других оно вычитается, так как находится в противофазе.

Рис. 4.6.4. Изменение звукового давления при изменении расстояния от оси при 120 Гц от 3-фазной ВЛ при сильном дожде при различных высотах от земли.
1 — на высоте 3 м; 2 — на высоте 0,75 м; 3 — на уровне земли; 4 — на высоте 1,5 м.
Небольшие изменения одного из параметров могут вызвать местные изменения уровня звукового давления до 20 дБ. Поэтому уровень звукового давления при шипении невозможно выразить одним значением. Огибающая максимальных значений на рис. 4.6.4 представляет собой максимально возможное значение звукового давления шума на частоте 120 Гц на заданном расстоянии от ВЛ. Этот максимум находится на уровне земли, когда волны, генерируемые средней и крайней фазами, в точке измерения имеют одинаковую фазу.
Рассчитанные значения максимально возможного звукового давления на расстоянии 15 м от крайней фазы будут даны в следующем разделе для основных конструкций ВЛ (см. рис. 4.6.20—4.6.24).
Следующий важный параметр, приведенный на этих рисунках, — наиболее вероятное значение на уровне земли. Оно рассчитывается в предположении случайного соотношения между фазами волн, приходящих в точку измерения от различных фазовых проводов ВЛ. В этом случае вычисляется давление для каждой фазы, а случайное значение получается при извлечении квадратного корня из суммы квадратов давлений каждой фазы.
Расчетные кривые звукового давления для «нормального» пучка и базовой конструкции ВЛ. Результаты получены для широкого ряда диаметров проводов пучка и их числа в фазе для «сильного дождя» и для «мокрого провода». Для упрощения принималось, что диаметр фазы постоянный (в соответствии с табл. 4.6.1).
Таблица 4.6.1

Акустический шум вычислен для максимального напряжения системы. Для более низких рабочих напряжений вводится поправка с помощью кривых, приведенных в следующем разделе. Результаты представлены на рис. 4.6.5—4.6.24.
Предполагаемая погрешность представленных данных ±3 дБ. Точность относительно базиса повышается, если сравниваются два провода. Результаты относятся к измерениям однодюймовым микрофоном, имеющим такие же характеристики направленности, как и микрофон General Radio (см. рис. 4.2.3).

Рис. 4.6.5. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 362 кВ.
1 — «сильный дождь»; 2 — «мокрый провод».

Рис. 4.6.6. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 550 кВ.
/, 2 —см. рис. 4.6.5.

Рис. 4.6.8. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 1200 кВ.
/, 2 — см. рис, 4-6.5.

Рис. 4.6.9. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 1500 кВ.
1,2— см. рис. 4.6.5.

Рис. 4.6.7. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 800 кВ.
/, 2 —см. рис. 4.6.5,

Рис. 4.6.10. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 362 кВ с низким реактивным сопротивлением.
1,2 — см. рис. 4.6.6.

Рис. 4.6.12. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 362 кВ с низким реактивным сопротивлением.

Рис. 4.6.11. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 362 кВ.
/, 2 — см. рис. 4.6.5.

Рис. 4.6.14. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 550 кВ с низким реактивным сопротивлением.
1,2 — см. рис. 4.6.5.

Рис. 4.6.16. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 800 кВ с малым реактивным сопротивлением.
1,2 — см. рис. 4.6.5.

Рис. 4.6.13. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 362 кВ.
1, 2 — см. рис. 4.6.6.

Рис. 4.6.15. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 550 кВ.
1,2 — см. рис. 4.6.6.

Рис. 4.6.17. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 800 кВ.
/1, 2 —* см. рис. 4.6.5.

Рис. 4.6.20. Зависимость звукового давления у земли при 120 Гц от диаметра провода фазы при сильном дожде, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 362 кВ.
1 — максимально возможные значения; 2 — наиболее вероятные значения.

Рис. 4.6.18. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 1200 кВ с низким реактивным сопротивлением.
1, 2 — см. рис. 4.6.5.

Рис. 4.6.19. Зависимость звукового давления от диаметра провода фазы, снятая на расстоянии 15 м от крайней фазы двухцепной ВЛ 1200 кВ.

Рис. 4.6.22. Зависимость звукового давления у земли при 120 Гц от диаметра провода фазы при сильном дожде, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 800 кВ.
1,2 — см. рис. 4.6.20.

Рис. 4.6.24. Зависимость звукового давления у земли при 120 Гц от диаметра провода фазы при сильном дожде, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 1500 кВ.

Рис. 4.6.21. Зависимость звукового давления у земли при 120 Гц от диаметра провода фазы при сильном дожде, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 550 кВ.
1,2 — см. рис. 4.6.20.

Рис. 4.6.23. Зависимость звукового давления у земли при 120 Гц от диаметра провода фазы при сильном дожде, снятая на расстоянии 15 м от крайней фазы одноцепной ВЛ 1200 кВ.
/, 2 — см. рис. 4.6.20.

Для микрофонов фирмы Bruel and Кlаer результат следует уменьшать на 1,5 дБ. Точка измерения обычно расположена на уровне земли, на расстоянии 15 м по горизонтали от крайней фазы. Результаты для «мокрого провода» зависят от состояния его поверхности. Приведенные на рисунках данные относятся к средней степени старения провода.
Влияние изменения параметров одноцепной ВЛ. Данные на рис. 4.6.5—4.6.9 получены для заданной конструкции ВЛ (высота подвеса, расстояния между фазами, диаметр фазы и напряжения). Положение и тип грозозащитных тросов незначительно влияют на шум, и этими факторами можно пренебречь.
Влияние других параметров приведено для одноцепной ВЛ разных напряжений и диаметров проводов в фазе, указанных в табл. 4.6.2.
Таблица 4.6.2

На рис. 4.6.25—4.6.49 как для «сильного дождя», так и для «мокрого провода» изменения шума обозначены как «добавка».
Влияние изменения параметров двухцепной ВЛ. На рис. 4.6.50 показано изменение поперечного горизонтального профиля звукового давления от ВЛ. Эти изменения добавляются к значениям на расстоянии 15 м.
Изменение шума при изменении других параметров (напряжения, геометрии линии, диаметра фазы) здесь не приводится из-за большой сложности вопроса для двухцепной ВЛ.
Предложен следующий порядок расчета.

1. Для заданной конфигурации вычисляются напряженности для каждой фазы.

Рис. 4.6.26. Влияние диаметра фазы ВЛ 362 кВ на изменение звукового давления.
/, 2— см. рис. 4.6.25.

Рис. 4.6.25. Влияние изменения напряжения ВЛ- 362 кВ на изменение звукового давления.
1,2 — см. рис. 4.6.5.

Рис. 4.6.27. Влияние междуфазных расстояний ВЛ 362 кВ на изменение звукового давления.

Рис. 4.6.28. Влияние средней высоты проводов ВЛ 362 кВ на изменение звукового давления.

Рис. 4.6.30. Влияние изменения напряжения ВЛ 550 кВ на изменение звукового давления.
1,2— см. рис. 4.6.25.

Рис. 4.6.33. Влияние изменения средней высоты подвески проводов ВЛ 550 кВ на изменение звукового давления.

1. — см. рис. 4.6.25.

Рис. 4.6.34. Влияние изменения расстояния измерителя от крайней

Рис. 4.6.38. Влияние средней высоты подвеса проводов ВЛ 800 кВ на изменение звукового давления.

1. 2 — см. рис. 4.6.25.

Рис. 4.6.36. Влияние диаметра фазы ВЛ 800 кВ на изменение звукового давления.
1,2 — см. рис. 4.6.25.
фазы ВЛ 550 кВ на изменение звукового давления.

Рис. 4.6.35. Влияние изменения напряжения ВЛ 800 кВ на изменение звукового давления.
1,2 — см. рис. 4.6.25.

Рис. 4.6.37. Влияние междуфазных расстояний ВЛ 800 кВ на изменение звукового давления. 7, 2 — см. рис. 4.6.26.

Рис. 4.6.40. Влияние изменения напряжения ВЛ 1200 кВ на изменение звукового давления.
J, 2 — см. рис. 4.6.25.

Рис. 4.6.29. Влияние изменения расстояния измерителя от крайней фазы ВЛ 362 кВ на изменение звукового давления.

Рис. 4.6.32. Влияние междуфазных расстояний ВЛ 550 кВ на измекение звукового давления.

Рис. 4.6.31. Влияние диаметра фазы ВЛ 550 кВ на изменение звукового давления.

Рис. 4.6.39. Влияние изменения расстояния измерителя от крайней фазы ВЛ 800 кВ на изменение звукового давления.

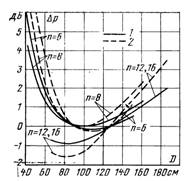
Рис. 4.6.42. Влияние междуфазных расстояний ВЛ 1200 кВ на изменение звукового давления. 1, 2 — см. рис. 4.6.25.
Рис._4.6.41. Влияние диаметра фазы ВЛ 1200 кВ на изменение звукового давления.
1,2+* см. рис. 4.6.25.
! ’ 'Т.ж>4
176

Рис. 4.6.44. Влияние изменения расстояния измерителей от крайней фазы ВЛ 1200 кВ на изменение звукового давления.

Рис. 4.6.46. Влияние диаметра фазы ВЛ 1500 кВ на изменение звукового давления.
/, 2 —см. рис. 4.6.25.
Рис. 4.6.49. Изменение      звукового

давления при изменении расстояния
Рис. 4.6.50. Изменение звукового давления при изменении расстояния измерителя для двухцепной ВЛ по рис. 4.6.10—4.6.19.

2.                       Для базовой конструкции, имеющей те же число и диаметр проводов в фазе, определяются напряженности.
3.                       Используя уравнение (4.5.3), для каждой фазы можно определить разность между шумами, создаваемыми для условий напряженности, вычисленных по пп. 1 и 2.
4.                       Находится среднее значение разницы, определенной в п. 3.
5.                       Поправку, вычисленную в п. 4, вводят к результату расчета профиля акустического шума для базисного случая (рис. 4.6.10—4.6.19 и 4.6.50).
Вычисление статистик акустического шума. В этом разделе предлагается модель погоды, основанная на опыте проектирования линии УВН.
Модель погоды, приспособленная к имеющимся в наличии данным, позволяет определить статистическое распределение уровня акустических шумов по метеорологической информации бюро погоды. Шум при любой плохой погоде относят к условиям сильного дождя, используя как параметр разницу С [в дБ (А)] между шумами при сильном дожде и мокром проводе.

Рис. 4.6.43. Влияние средней высоты подвеса проводов ВЛ 1200 кВ на изменение звукового давления. 1,2— см. рис. 4.6.25.

Рис. 4.6.45. Влияние изменения напряжения ВЛ 1500 кВ на изменение звукового давления. 1,2— см. рис. 4.6.25.

Рис. 4.6.48. Влияние средней высоты проводов ВЛ 1500 кВ на изменение звукового давления.

Рис. 4.6.47. Влияние междуфазных расстояний ВЛ 1500 кВ на изменение звукового давления.
/, 2 — см. рис. 4.6.25.

При сильном дожде получено распределение уровней шума, приведенное в табл. 4.6.4.
Если С=6 дБ, получим распределение, показанное на рис. 4.6.51.
Распределение, подобное приведенному на рис. 4.6.51, возможно определить для любого места, для которого имеются метеорологические данные, и при любом значении параметра С. Таким образом могут быть рассчитаны только характеристики шума линии при «сильном дожде» и для условий «мокрого провода».
Следует отметить, что использованная здесь модель погоды нуждается в совершенствовании. В частности, ошибочно предположение, что во время Дождя провод весь мокрый, В реальных условиях при слабом дожде требуется значительное время для попадания воды между проволоками.                                                                                                                                                

Примечание. общее. число часов плохой погоды приведено ниже
для разной погоды:
Дождь                                                     475
Снег                                                         90
После дождя                                         71
туман                                                       170
После тумана                                        80

Рис. 4.6.51. Статистическое распределение изменения звукового давления по отношению к «сильному дождю», определенное с модели погоды, С*=6 дБ,

Следовательно, в течение длительного времени при дожде шум будет ниже уровня, соответствующего «мокрому проводу». По мере накопления статистических данных для 3-фазных линий при различных климатических условиях понимание этого вопроса станет более полным.

Статистический анализ слышимого шума дается в [8, 21]. Полученные результаты приведены на рис. 4.6.52. Они показывают проценты плохой погоды, при которой шум превышает значения, указанные по оси ординат.
Рис. 4.6.52. Функция распределения акустического шума 3-фазной ВЛ 775 кВ при дожде.
1 —1X2,5; 2 — 2Х 1,602; 3 — ЗХ XI,30; 4 — 4X1; 5 — 4x1,196; 6 — 4x1,38.
Данные, приведенные на рис. 4.6.52, сравнивались с вычисленными с помощью рис. 4.6.6 и 4.6.7. При этом были введены поправки по рис. 4.6.30, 4.6.32, 4.6.34, 4.6.35 и на использование микрофона Bruel and Кlаёr вместо General Radio. Учитывалось также затухание в 1 дБ вследствие защиты микрофона кожухом (по данным [21]). Результаты приведены в табл. 4.6.5.
Таблица 4.6.5

В таблице приведена разница значений С, рассчитанных для шумов при «сильном дожде» и «мокром проводе». Для сравнения приведена разница между 95 и 50%- ными значениями величин по рис. 4.6.52. Очевидно, достигнута отличная корреляция между этими величинами. Таким образом, статистическое распределение слышимого шума при дожде может быть получено по опытным данным при «сильном дожде» и «мокром проводе». Чем больше разница шумов при «сильном дожде» и «мокром проводе», тем большее рассеяние будут иметь величины слышимого шума, измеренного в дождь. По-видимому, слышимый шум при «мокром проводе» соответствует 50%-ному значению на кривой статистического распределения при дожде.