- ПОТЕРИ НА КОРОНУ
Поле в отсутствие короны. Электрическое поле Е= _—у у в отсутствие короны описывается уравнением Лапласа V2V=0. Расчеты, проводимые в соответствии с этим уравнением, позволяют оценить напряженности возникновения короны. В большинстве практических случаев расчет ведется для поля Лапласа, а не для тока сложного поля с объемным зарядом, которое формируется в условиях короны. Например, в основе построения проектных кривых для радиопомех, акустических шумов и потерь на корону, приведенных в последующих главах, лежит значение поверхностной напряженности, рассчитанной в предположении отсутствия короны. И хотя в этих случаях расчетная напряженность не отражает подлинной картины поля, ее использование является удобным для описания рассматриваемого явления.
При наличии неровностей на поверхности, таких, например, как капли воды, начало коронного процесса определяется напряженностью, соответствующей этим неровностям. Его значение оценить очень трудно, и в обычной расчетной практике используется напряженность, соответствующая гладкой поверхности провода.
Капли воды на проводе с точки зрения формирования электрического поля сходны с коническими выступами. Максимальные напряженности соответствуют тем точкам, где концентрация эквипотенциальных линий наибольшая. Наивысшая интенсивность поля отмечается в непосредственной близости от проводов. Коронный разряд, такой, например, как положительный стример, может распространяться на длину одного-двух диаметров от поверхности провода и достигать точек, где потенциалы в отсутствие короны на 5—10% ниже потенциала провода. Ток короны в значительной степени зависит от этого перепада потенциалов.
Таким образом, если рассматривать два провода различного диаметра, имеющие, однако, одинаковые поверхностные напряженности, то коронный импульс и его
развитие будут интенсивнее для провода с большим диаметром.
Поле при наличии короны. Ток короны. Проблема описания поля при наличии объемного заряда является крайне сложной. Этим объясняется малое количество данных, имеющихся в литературе об искажении поля объемным зарядом, образующимся при короне.
Для исследования потерь на корону необходимо провести расчет поля при наличии объемного заряда, по крайней мере в непосредственной близости от проводов. Немного дальше поле может уже рассматриваться без учета объемного заряда с небольшим лишь дополнительным его перемещением, представляющим собой ток короны.
Как пример искажения поля вокруг провода при короне было проанализировано поле Пойссона для концентрических цилиндров со свободными зарядами.
Радиус внутреннего провода 0,9 см, радиус внешней оболочки цилиндра 26 см.
В качестве критерия возникновения свободного заряда был применен закон Пика
![]() (2.3.1)
(2.3.1)
где 6— относительная плотность воздуха, равная 1; М — коэффициент неровности поверхности (равный 0,5); R — радиус провода (равен 0,9 см).
Подставляя эти значения в (2.3.1), получаем Ег,та%= = 19 700 В/см.
Значение пространственного заряда, образующегося в каждый интервал времени, подсчитывалось в предположении [2.8], что поверхностная напряженность никогда не может превысить EГ)ШД. Подвижность ионов была определена на экспериментальной установке: для отрицательных ионов она составляла 1,99 (см/с) / (В/см), для положительных ионов 1,40 (см/с) / (В/см). Спустя три периода после подачи напряжения величины плотности заряда, тока и потенциала становятся периодическими. Четвертый период напряжения и тока показан на рис. 2.3.1. На рис. 2.3.2 изображены также для сравнения потенциальные ноля по Лапласу. На рис. 2.3.3 представлен характер распределения свободного заряда.
Как видно из рис. 2.3.1, ток короны в основном совпадает по фазе с приложенным напряжением. Он имеет также емкостную составляющую, которая, однако., незначительна по сравнению с емкостным током в проводах в отсутствие короны.
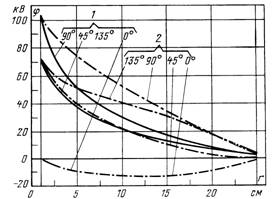
Рис. 2.3.2. Потенциальные поля короны при цилиндрической соосной конфигурации электродов.
1 — потенциал в отсутствие короны; 2 — потенциал при наличии короны.
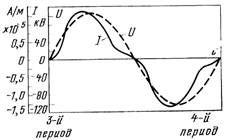
Рис. 2.3.1. Ток короны при цилиндрической соосной конфигурации электродов (потери на корону 61,5 Вт/м).
Мощность потерь может быть вычислена интегрированием произведения мгновенных величин напряжения и тока в пределах периода. В примере на рис. 2.3.1 вычисленные потери составляют 61,5 Вт/м. Потенциальное поле короны вблизи провода воздушной линии электропередачи переменного тока имеет вид, схожий с тем, что изображен на рис. 2.3.1 — 2.3.3. По мере удаления от провода вследствие рекомбинации ионов поле становится все более свободным от объемного заряда, приближаясь к полю Лапласа. Однако в силу перемещения зарядов возникают потери, а потенциалы и напряженности незначительно возрастают.
Потери на корону при хорошей погоде. Первые исследования потерь на корону на линиях передачи переменного тока начались в Соединенных Штатах еще в начале века. Эти исследования носили, однако, спорадический характер вплоть до окончания второй мировой войны, когда возникла необходимость в передачах СВН.
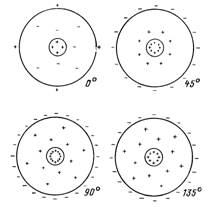
Рис. 2.3.3. Пример распределения свободного заряда в зависимости от фазы приложенного напряжения.
Соответствующий опыт был приобретен в основном на исследованиях, проводившихся на трех испытательных комплексах СВН: Проекте Тидда [2.9, 2.10] и установке «Эппл Гроув», которые были организованы Американской энергетической корпорацией и фирмой «Вестингауз», а также на установке СВН фирмы «Дженерал электрик».
В 1911 г. Пик и его сотрудники обнаружили, что для чистых сухих проводов потери на корону в установившемся режиме промышленной частоты могут быть выражены соотношением вида, кВт:
![]() (2.3.2)
(2.3.2)
где К — постоянная; U — действующее напряжение провод— земля, кВ; U0 — действующее напряжение про-
вод — земля, соответствующее началу коронного процесса (начальное напряжение короны, кВ).
Однако квадратический закон оказывается недействительным в области напряжений, близких к напряжению начала коронного процесса. В 1924 г. была предложена зависимость для потерь при хорошей погоде в виде
![]() (2.3.3)
(2.3.3)
где f — частота приложенного напряжения; С — емкость системы провод — земля; Uo— начальное напряжение короны.
Поскольку P=U/, можно предположить, что величина 4fC(U—Uo) представляет собой эквивалентный ток короны. В 1927 г. Хольмом было проведено теоретическое исследование механизма потерь на корону в поле двух параллельных проводов; полученное им выражение мощности потерь оказалось сходным с (2.3.3).
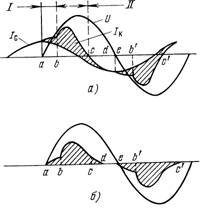
Рис. 2.3.4. Теоретические формы волн емкостного тока (а) и тока короны (б) в поле параллельных проводников (по Хольму).
1 — область тока остаточных ионов; II — область тока короны.
Изображенная на рис. 2.3.4 кривая тока, построенная Хольмом в соответствии со своими расчетами, полностью соответствует кривым тока, снятым экспериментальным путем на испытательных установках Проекта СВН [2.12, 2.13]. На рис. 2.3.4,а представлены обе теоретические кривые — емкостного тока и тока короны, на рис. 2.3.6,6
кривая емкостного тока опущена и изображена лишь кривая тока короны.
В 1933 г. во время дискуссии в Американском институте инженеров-электриков Петерсон предложил формулу потерь на корону в однофазном поле при хорошей погоде, которая с тех пор стала классической, кВт/км:
![]() (2.3.4)
(2.3.4)
где1 — промышленная частота, Гц; U — действующее напряжение относительно земли, кВ; 5 — расстояние между проводами, м; d — диаметр провода, см; F — коэффициент короны, определенный экспериментально и являющийся функцией отношения U/Uo.
Поскольку, однако, потери на корону при хорошей погоде для большинства линий СВН не имеют серьезного практического значения, приведенные выше формулы применяются редко. Потери, связанные с токами утечки через изоляторы, имеют для этих линий тот же порядок, что и потери на корону при хорошей погоде, однако потери в изоляторах зависимостью Петерсона не учитываются. Потери на корону при дожде или снеге во много раз превосходят потери при хорошей погоде, и именно им было уделено много внимания при исследованиях на опытных линиях [2.12—2.17].


