ПРИЛОЖЕНИЕ IX ГИДРАВЛИКА ПОЙМЕННОГО МАССИВА
IX.1. Гидравлическая схема затопления и опорожнения пойменного массива
IX.1.1. Движение воды в затопленных поймах равнинных рек и по общей направленности процесса, и по деталям строения скоростного поля существенно отличается от течения в речном русле. При построении теоретических и расчетных схем в этом случае следует избегать русловых аналогий, к которым склоняет большая их изученность.
Если морфологическое строение речного русла находится в полном соответствии с формирующим его потоком, то морфология поймы представляет некоторую стадию переработки пойменными потоками рельефа, первоначально унаследованного у реки. Пойменный поток в этих условиях сочетает в различных соотношениях черты русловых потоков п черты водоемов. При этом возникают и такие гидравлические фрагменты, которые несвойственны ни руслам, ни водоемам.
Многорукавные поймы можно схематически представить как сеть однонаправленных, взаимопересекающихся каналов. В отличие от этого, для пойм свободно меандрирующих рек характерны застойные зоны, обладающие значительной аккумулирующей емкостью. Протоки или отсутствуют, или намечаются на отдельных, относительно коротких участках. Они или приспосабливаются к несвойственным им унаследованным формам (староречьям, пониженным междувальям), пли стремительно преодолевают пойменные преграды, имеющие вид береговых валов и внутрипойменных грив.
Разнообразие и недостаточная отчетливость морфологического строения пойм, наличие большого количества различных гидравлических фрагментов исключают возможность на современном уровне наших знаний создание единой общей гидравлики пойм. Вместе с тем полезно рассмотреть некоторые частные, но достаточно распространенные случаи. Если при этом не всегда удается достигнуть полного законченного гидравлического расчета или в силу принципиальных трудностей, или в силу большой трудоемкости расчетов и затруднений с получением исходных материалов, то это все же расширяет представление о процессе и позволяет с достаточной точностью отвечать на некоторые частные вопросы.
Ниже рассматривается гидравлическая схема затопления и опорожнения пойменного массива свободно меандрирующей реки. Этот процесс представляет интерес и в силу его большой распространенности, и потому, что в нем получают четкое выражение некоторые элементы, характерные для пойменного процесса вообще.
IX.1.2. Пойменный массив. Извилистое русло меандрирующей реки на отдельных своих участках приходит в соприкосновение с коренным берегом долины.
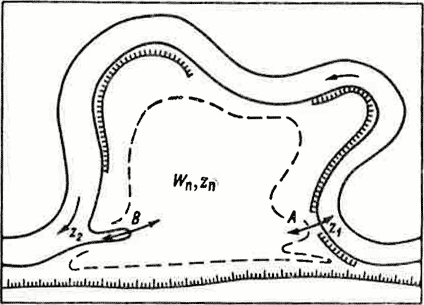
Рис. IX-1. Схема простейшего пойменного массива при свободном меандрировании.
Две смежные точки такого соприкосновения русла с одним склоном (правым или левым) выделяют замкнутый пойменный массив, ограниченный с одной стороны склоном долины и с другой — меандрирующим руслом. При ограниченном меандрировании каждой излучине соответствует свой пойменный массив и морфологическое строение такого массива обладает и наибольшей простотой и наибольшей определенностью. При свободном меандрировании сближение русла с одним и тем же склоном долины происходит на участке русла, включающем ряд излучин. Если этот участок невелик и включает лишь несколько (три-четыре) излучин, то морфологическое строение пойменного массива сохраняет некоторые общие черты, свойственные массивам этого рода и представляющие некоторое развитие и усложнение массива рек с ограниченным меандрированием. Эти общие черты сводятся к следующему (рис. IX-1). Наиболее повышенной оказывается полоса, расположенная вдоль русла реки. Обычно она имеет вид более или менее четко выраженного берегового вала. Центральная часть массива, примыкающая к краю долины, понижена и особенно с низовой стороны. В этом сходство массива свободно меандрирующих рек и рек с ограниченным меандрированием. Различие же состоит в том, что весь рельеф поймы при свободном меандрировании значительно усложнен наличием внутрипойменных грив, в результате чего вся пониженная часть массива может оказаться расчлененной на изолированные области. Затопление и опорожнение центральной части массива и отдельных его изолированных частей происходит через местные понижения в береговых валах и внутрипойменных гривах. В этих местах сосредоточивается главная часть падения уровня воды, приходящегося на весь пойменный массив. Скорости течения в этих местах могут достигать сверхкритических величин и на них приходится главная часть расхода всего пойменного массива. Эти понижения в пойменных преградах получили характерное народное название прорвы.
Наличие больших пониженных областей, соединенных отдельными протоками, сообщает пойменному массиву способность наряду с пропуском высоких вод оказывать и аккумулирующее действие, величина которого зависит от размеров аккумулирующих емкостей.
Представляется целесообразным выделить три типа прорв:
1) верховые, 2) низовые и 3) внутрипойменные.
Верховые прорвы располагаются в верховой части массива в береговых валах, там, где эти валы имеют наибольшую высоту (рис. IX-1, точка А). Эти прорвы, как и прорвы других типов, на разных фазах затопления и опорожнения поймы могут пропускать воду в противоположных направлениях — в направлении из русла в пойму при затоплении массива и в обратном направлении при его опорожнении. Но суммарный объем воды, поступающей в пойму в этих прорвах, всегда больше, чем объем воды, вытекающей из поймы. В этом заключается гидрологический признак верховой прорвы. Морфологическая особенность ее заключается в наличии гребня и двух склонов, обращенных один в сторону реки, другой в сторону поймы. Верховые прорвы часто размещаются против плёсовых ложбин, где в паводок циркуляционные и турбулентные процессы в потоке имеют наибольшее развитие и это способствует выносу в пойму через верховые прорвы значительного количества песка.
Низовые прорвы расположены в низовой части массива. Они имеют вид протока, по которому вода стекает с поймы до полного ее опорожнения. Это значит, что эта прорва или не имеет гребня, или гребень ее расположен низко и отчленяет существующее в этом случае пойменное озеро (рис. IX-1, точка В).
IX. 1.3. Принципиальная схема затопления и опорожнения пойменного массива. Эта схема легче всего поясняется на простейшем примере, изображенном на рис. IX-1, на котором представлен пойменный массив, имеющий одну пойменную емкость, одну верховую прорву и одну низовую. Гидравлическими характеристиками массива являются кривая зависимости объема пойменной емкости W от отметки уровня воды в пойме (рис. IX-2) и график зависимости расхода воды Q через прорву от положения уровня воды в реке и в пойме. Такой график строится на основании гидравлического расчета для верховой и низовой прорв. Примерный вид такого графика показан на рис. IX-3. Подробно о его построении говорится в п. IX.2.
Схема затопления и опорожнения пойменного массива показана на рис. IX-4. На верхнем рисунке показан ход уровня воды в русле на участке верховой прорвы (кривая z1) и участке низовой прорвы (кривая z2) за время прохождения паводка. Обе эти кривые совпадают по фазе, но вторая из них снижена относительно первой на величину падения уровня воды в реке в пределах рассматриваемого массива.
Затопление поймы начинается с низовой прорвы тогда, когда уровень воды в этом месте реки Z2 становится выше отметки гребня низовой прорвы zn (или наинизшей отметки поймы).
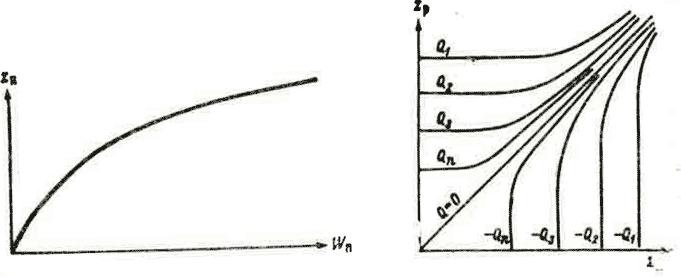
Рис. IX-2. Зависимость объема пойменной емкости И:'п от отметки уровня воды и пойме z.
Рис. IX-3. Зависимость расхода воды Q через прорву от отметок уровней воды в реке и в пойме.
На графике 1Х-4 этот момент обозначен точкой а. В этой начальной фазе уровень воды в реке выше уровня воды в пойме zu и расход воды в сторону поймы Q, на рассматриваемой схеме условно считается положительной величиной. С момента, когда уровень воды в русле реки у верховой прорвы Z поднимается выше отметки гребня верховой прорвы, начинается перелив через эту прорву из реки в пойму. На рис. 1X-4 этому моменту соответствует точка б. Расход Qn в это время тоже положителен.
С начала работы верховой прорвы наступает второй период цикла, характерный тем, что уровень воды в пойме zn начинает расти быстрее, чем в русле у низовой прорвы. Этот период заканчивается тогда, когда значения выравниваются (на рис. IX-4 точка с). Дальнейший рост уровня в пойме приводит к тому, что низовая прорва начинает работать в обратном направлении и расход волы Q меняет знак с положительного на отрицательный. Пойма начинает участвовать в пропуске паводочных вод. Этот третий период цикла характерен тем, что z1>zn; zп>z2, QB>0; QH<0. Третий период закапчивается тогда, когда уже на спаде паводка происходит выравнивание уровней (на рис. IX-4 точка d). Падение уровня в реке идет быстрее, чем в пойме и на этом коротком четвертом этапе верховая прорва работает в обратном направлении, отдавая воду обратно реке. Этот этап заканчивается моментом, когда уровень воды в пойме выравнивается с отметкой гребня верховой прорвы zB (на рис. IX-4 точка е). С этого момента верховая прорва обсыхает и дальнейшее освобождение поймы от воды происходит только через низовую прорву.
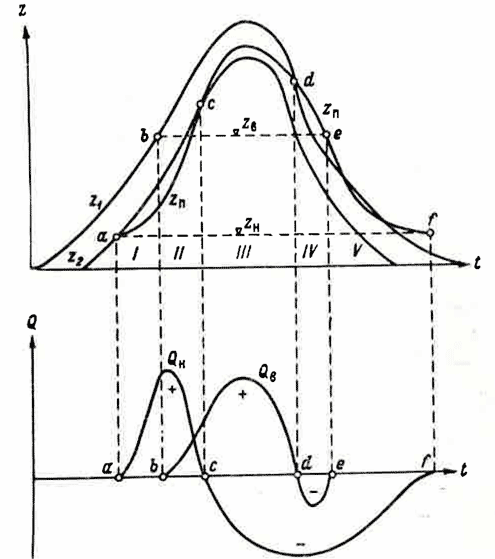
Рис. IX-4. График уровней и расходов при затоплении и опорожнении пойменного массива.
Из представленной схемы следует, что из всего объема воды, поступившей на пойменный массив за время прохождения паводка, лишь часть воды представляет транзитный расход. Остальная часть аккумулируется поймой. Объем транзитной воды WT равен разности объемов воды, прошедшей через прорву в противоположных направлениях. Эта разность одинакова по абсолютной величине и для верховой и для низовой прорв![]() и аналитически выражается так:
и аналитически выражается так:
Объем аккумуляции Wa равен сумме двух объемов в абсолютном выражении — объема воды WB, поступающей на пойму через
низовую прорву, и объема воды Wn, поступающей из поймы в реку через верховую прорву, т. е.
![]()
пли
![]()
Для графика расходов, изображенного на рис. IX-4, отношение Wt равно приблизительно 1: 0,85, т. е. объем аккумуляции по величине близок к величине транзитного объема. В настоящее время мы не располагаем достаточными обработанными материалами по затоплению пойменных массивов свободно меандрирующих рек для того, чтобы ответить на вопрос, насколько характерно для существующих пойм это приведенное отношение объема транзита и объема аккумуляции.
Транзит поды через пойменный массив происходит только в течение третьего периода, т. е. тогда, когда расход верховой прорвы положителен, и одновременно с этим расход низовой прорвы отрицателен. Транзитный расход Qr равен наименьшему из абсолютных значений этих двух расходов.
Из рассмотренной схемы затопления и опорожнения поймы вытекает и схема расчета этого процесса. При расчете используются следующие исходные данные:
- характеристика аккумулирующей емкости пойменного массива (рис. IX-2) zn—f(W)\
- гидравлические характеристики верховой и низовой прорв (рис. IX-3): Qa=f(zuz„), Q„ = /(z2, zn);
- гидрологические характеристики расчетного паводка (рис. IX-4): z, = ф (t), г2 =(р (/).
Первая из приведенных зависимостей предполагает отсутствие уклона свободной поверхности в аккумулирующей емкости и это положение приходится принимать как упрощающее допущение, по- видимому, весьма близкое к действительности.
Целью расчета является получение зависимостей
![]()
Так как исходные данные относятся к природным явлениям и не имеют общего аналитического выражения, то задачу приходится решать в конечных разностях. Ход решения задачи поясняет приведенная ниже табл. IX-1.
В графиках 1—3 этой таблицы приводятся исходные гидрологические данные, выражающие изменение во времени уровня воды в реке на участках верховой и низовой прорв.
В первой строке граф 4 и 5 дается положение уровня воды в пойме и объем заполнения поймы Wп в начальный момент ; эти данные также являются заданными начальными условиями. Они позволяют определить среднюю величину расхода воды через верховую и низовую прорвы за интервал времени t.
Таблица IX-1
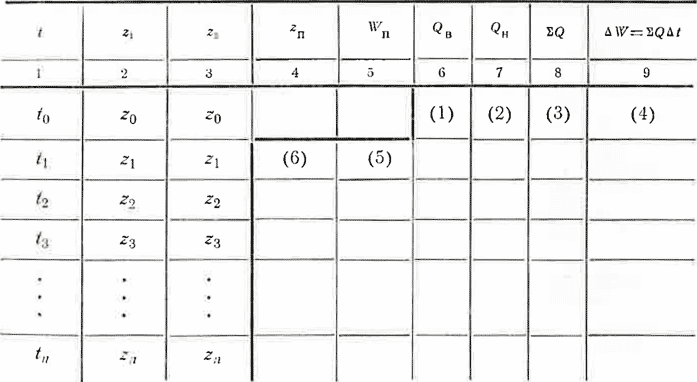
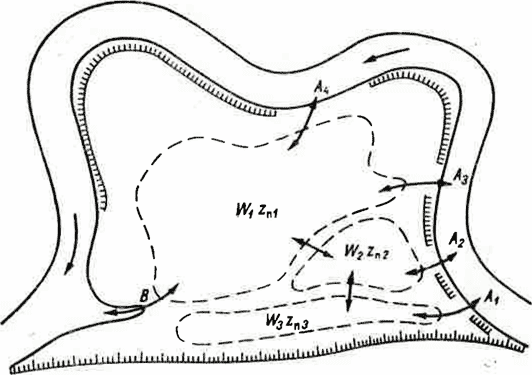
Рис. IX-5. Схема сложного пойменного массива при свободном меандрировании.
Эти величины приводятся в графах 6 и 7. Суммарный расход QB приводится в графе 8. Этот расход, умноженный на интервал времени At, определяет изменение пойменной емкости (графа 9) и позволяет вычислить пойменную емкость в момент t1. Это значение Wn записывается в соответствующей строке графы 5. По нему определяется положение уровня воды в пойме (графа 6) и вычислительные операции подобным способом повторяются для интервала времени. В этом же порядке производится и весь последующий расчет.
Интервалы времени следует выбирать достаточно малыми, чтобы неучет изменения положения уровней воды в течение интервала времени At не оказывал заметного влияния на определение величин Q. В противном случае следует вычислить эти величины по втором приближении. Весь ход задачи остается принципиально тем же, но технически усложняется, если в пойменном массиве имеется несколько емкостей и несколько прорв (рис. IX-5).
В прорвах, особенно в верховых, возможно возникновение стремительных потоков с большими скоростями течения. Эти большие скорости могут образовывать большие местные размывы, следы которых часто и обнаруживаются в поймах. В тех случаях, когда береговые валы или прорвы имеют травяной покров, они способны выдерживать значительные скорости. По американским данным (В. Т. Чоу «Гидравлика открытых каналов»), некоторые травы выдерживают скорости до 2,5 м/с. Но эта способность сразу резко снижается при нарушении травяного покрова. Известны случаи возникновения неожиданных больших размывов в поймах и занесения песком больших участков ее поверхности, вызванные обращением лугов в огородные участки и нарушением целости береговых валов.
IX.2. Перелив воды через пойменные преграды
IX.2.1. Одним из основных элементов общего гидравлического процесса в затопляемых поймах является перелив воды через пойменные преграды, под которыми понимаются береговые валы, внутрипойменные гривы и прорвы, т. е. пониженные участки этих преград. Здесь сосредоточивается главная часть падения уровней воды между створами, ограничивающими пойменный массив, и скорости течения здесь могут достигать сверхкритических величин, т. е. на много превосходить скорости течения в основном русле.
Детальный гидравлический расчет потока на пойменной преграде затруднен неопределенностью и Неустойчивостью морфологического очертания валов и прорв и наличием таких трудно учитываемых факторов, как состояние растительности.
В приведенном ниже примере допущена упрощенная схематизация явления, позволяющая выявить основные свойства процесса и получить приблизительную его количественную оценку.
Преграда в продольном разрезе (по направлению течения) представляется в виде горизонтального гребня и двух склонов прямолинейного очертания. По ширине форма препятствия остается неизменной и задача решается в двухмерной постановке (рис. IX-6). Весь участок преграды ограничен двумя створами, уровни воды в которых в рассматриваемой задаче считаются заданными величинами. В процессе заполнения и опорожнения поймы соотношение уровней и может меняться, т. е. условие может меняться, и течение через преграду при этом будет менять свое направление.
Размеры преграды, крутизна склонов, превышение уровня воды над отметкой гребня zr могут меняться в широких пределах. При этом однако сохраняются некоторые особенности, характерные для пойменных преград, которые сужают границы задачи и вместе с тем выделяют области, требующие большого внимания.
Эти особенности сводятся к следующему. Уклоны откосов i1 и i3, как правило, на один или на несколько порядков больше, чем уклоны в реке. Длина горизонтального гребня невелика по сравнению с наибольшим возможным превышением уровня воды в верховом створе над отметкой гребня. Общий перепад уровней обычно невелик. Он в редких случаях превосходит падение уровня воды в реке в границах пойменного массива, т. е. Обычно выражается величиной, не превышающей 1—2 м.
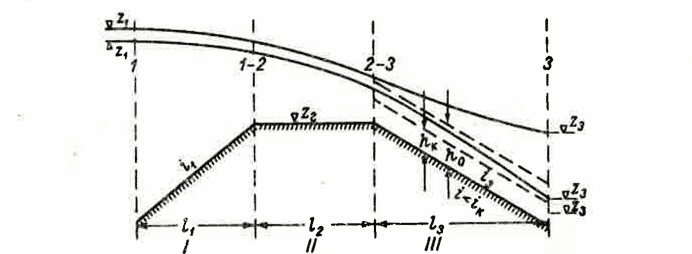
Рис. IX-6. Возможная форма свободной поверхности при В особо редких случаях эта величина может быть превзойденной, например, в верховой прорве большого пойменного массива с большой пойменной емкостью и малой пропускной способностью низовых прорв. Нельзя исключать случая и полного перекрытия низовых прорв. Если уклоны больше,
чем 0,1, а длина гребня <10(z1— z), то препятствие можно рассматривать как водослив. Если же это условие не выполнено — задачу приходится рассматривать как неравномерное движение в канале с переменным уклоном дна.
Задача расчета заключается в определении расхода воды через препятствие в зависимости от положения уровня воды в створах 1 и. 3 и в оценке возможных наибольших скоростей течения, возникающих в струе, сходящей с преграды. Так как задача рассматривается в двухмерной постановке, то расход воды определяется его удельным значением q м2/с. Результат расчета выражается семейством кривых, определяющих связь отметок z для различных значений q. Связь этих величин графически выражается с большей точностью, если за одну координату принять отметку z, а за вторую координату изменения z, выразив ее в логарифмической шкале.
В действительных условиях явление усложнено рядом обстоятельств, не учтенных в настоящей схеме. В частности, подход
потока к преграде может быть боковым, что особенно сильно выражается при переливе воды из основного русла через береговой вал.
1Х.2.2. Водослив. Расход воды через преграду рассчитывается по схеме водослива. По Н. Н. Павловскому, расход воды через такую преграду может рассчитываться по формуле
![]() (IX-1)
(IX-1)
Рекомендуемые значения коэффициентов т в зависимости от величин z, приводятся в табл. IX-2. Знаком плюс ( + ) отмечены условия, при которых для расчета рекомендуется формула водослива с широким порогом.
Таблица IX-2

Учет подтопления водослива, определение формы сопряжения струи с нижним бьефом и максимальной скорости в струе, сходящей с водослива, производится по общим правилам расчета водослива.
IX.2.3. Форма свободной поверхности потока, переливающегося через преграду. В тех случаях, когда по условиям, приведенным в п. IX.2.2, преграда не может рассматриваться как водослив, ее приходится рассматривать как канал с меняющимся уклоном дна и гидравлический расчет вести по формулам неравномерного движения. На участке I и на участке II свободная поверхность во всех случаях имеет форму кривой спада. На участке III тип кривой свободной поверхности будет зависеть от того, лежит ли нормальная глубина выше или ниже критической глубины hK, и в какой зоне лежит уровень воды в створе 3. Так как соотношение ho и hк меняется при различных расходах, то и поток на участке III будет или спокойным или стремительным в зависимости от величины расхода.
Для расходов, при которых ho>hK (спокойный поток), возможны лишь два вида кривой свободной поверхности. При z3>h0
устанавливается кривая подпора, которая распространяется до створа 2—3. Выше этого створа, на участках II и I, устанавливаются кривые спада, которые и определяют уровень воды в створе I. В этом створе уровень воды всегда оказывается выше критической глубины и этот уровень определяет положение уровня и в створе 1. Если за створом 3 уровень воды лежит ниже критической глубины, то характер кривой спада сохраняется, и в конце участка образуется местный перепад (рис. IX-6).
При расходах в случае, если Z3<(zr+hK), участок III работает как быстроток. Уровень воды в створе 3 не оказывает влияния на участок 2, в конце которого
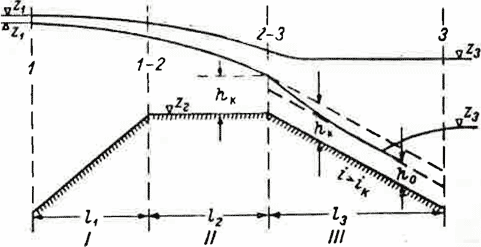
Рис. 1Х-7. Возможности формы свободной поверхности при <3>iK.
устанавливается критическая глубина. В верховой части участка III образуется кривая спада, по которой поток быстро переходит от критической глубины к нормальной. С уровнем створа 3 поток сопрягается прыжком и кривой подпора. Картина меняется лишь при условии, когда нижний бьеф подтапливает критическую глубину на гребне. С практической точки зрения этот случай представляет значительный интерес, поскольку возникновение его при затоплении и опорожнении пойменного массива весьма вероятно. Гидравлическое же решение такой задачи не обладает достаточной определенностью, и поиски строгого решения находились бы в противоречии с грубой схематизацией явления, к которой приходится прибегать в рассматриваемом случае. Для практического решения задачи некоторые авторы рекомендуют формулу затопленного водослива с широким порогом
![]() (IX-2)
(IX-2)
Другой прием заключается в том, что на участке III кривая подпора заменяется горизонтальной прямой и уровень переносится в створ. Такой прием оправдывается тогда, когда подъем уровня в пределах участка III невелик и им можно пренебречь, особенно учитывая, что сопряжение стремительного потока с кривой подпора сопровождается трудно учитываемыми местными потерями.
Большие уклоны низовой грани приводят к возникновению особого случая, мало распространенного в инженерной гидравлике. В начале перелива через гребень, при малых расходах воды, поток имеет характер спокойного течения. При увеличении расхода поток переходит в стремительное состояние.
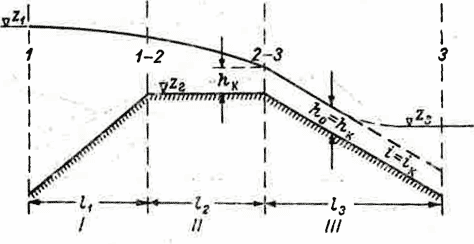
Рис. IX-8. Форма свободной поверхности при 13=in-
В значительном диапазоне расходов режим течения оказывается близким к критическому и разница между ho и hк весьма небольшая. В этой области свободная поверхность потока по своему виду близка к тому, что теоретически соответствует критическому режиму, при котором на участке, лежащем выше уровня, устанавливается нормальный режим, т. е. ho = hu, а при достижении уровня z свободная поверхность сразу переходит в горизонтальную прямую (рис. IX-8).
В действительности такая теоретическая картина сопряжения двух участков не выдерживается, поскольку здесь нарушается условие медленно изменяющегося движения. На практике же приходится считаться с тем, что переход от свободной поверхности равномерного течения к горизонтальной свободной поверхности происходит на коротком участке и этот вид сопряжения сохраняется и в области, где глубины ho и hK близки по своим значениям.
Порядок гидравлического расчета пойменной преграды поясняется на частном примере, условия которого можно считать характерными для пойменных преград.
IX.2.4.1. Пример гидравлического расчета пойменной преграды. При гидравлическом расчете пойменной преграды заданными величинами являются размеры преграды и предельные значения
уровней воды в крайних створах.
В примере рассматривается движение и направление от створа 1 к створу 3. Расчет обратного движения производится тем же способом. Гребню преграды придаем условную высотную отметку 3,00 м. Предельные положения уровней воды в створах 1 и 3 в той же системе отметок имеют следующие значения: Z1 = 3,00-4,50 м, 23 = 0,00-4,50 м.
Показатель шероховатости п = 0,03; корректив на неравномерность распределения скоростей 1,1.
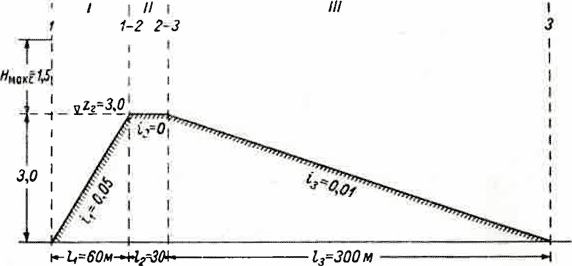
Рис. IX-9. К примеру гидравлического режима пойменной преграды.
Целью расчета является: 1) получение зависимостей, позволяющих по заданным значениям z определять величину расхода через преграду; 2) оценка возможных наибольших скоростей течения в струе, сходящей с порога. При заданных условиях в ряде случаев эти скорости окажутся значительно превосходящими величину размывающих скоростей. В этих случаях преграда оказалась бы неустойчивой, что в действительности и может встречаться. Однако действительные возможные сочетания Z устанавливаются общим расчетом затопления и опорожнения пойменного массива и искомые в настоящей задаче зависимости q=f(z\z3) должны рассматриваться как оперативное средство для решения общей задачи.
Путь разрешения этой частной задачи в принципе заключается в том, что для заданного расхода qn по заданному значению определяется значение z, в створе 2—3, используя уравнение неравномерного движения; подобным же образом по отметке z2-3 определяется отметка уровня в створе 1—2 и отсюда тем же способом отметка z1. Таким образом устанавливается соотношение между отметками z для расхода qn при выбранном значении.
Расчет повторяется для ряда значений в необходимом диапазоне этих значений. Затем подобный расчет повторяется для других значений q. Диапазон значении задан. Остается неясным предел значений q, который может быть выяснен только в процессе расчета по предельно высокому значению.
Техническая часть расчета сводится к выбору такой последовательности вычислительных операций, при которой сокращается объем вычислений и в первую очередь путем исключения тех вычислений, которые не дают практически полезных результатов.
IX.2.4.2. Участок II. Решение целесообразно начать с участка II, в пределах которого устанавливается всегда кривая спада. Значения h, вычисленные по формуле
![]()
(IX-4)
приведены в табл. IX-3. В этой же таблице приведены значения критических уклонов iK, вычисленных по формуле
![]()
(IX-5)
Таблица 1Х-3



