Основы теории электрических аппаратов - Моделирование нагревания аппаратов, нагревание нетоковедущих частей аппаратов

§ 11.9. МОДЕЛИРОВАНИЕ НАГРЕВАНИЯ АППАРАТОВ

Тепловой расчет отдельных токоведущих частей аппаратов может быть произведен с достаточной степенью точности при помощи приведенных ранее формул. Расчет же целых аппаратов крайне труден и не всегда возможен. Поэтому нагревание аппаратов, как правило, определяется опытом. Но при больших токах, на которые уже в настоящее время приходится строить аппараты (15-:-25 кА), такие опыты очень дороги. С целью уменьшения стоимости испытания аппаратов стремятся их моделировать. Теория подобия указывает условия, при которых возможно такое моделирование.
Ранее указывалось, что существует автомодельная область, определяющаяся значениями Gr-Pr >2· 107. В ней процесс конвективного теплообмена не зависит от определяющего размера нагретого тела. Так как теплоотвод через излучение, отнесенный к единице поверхности нагретого тела, также не зависит от размеров этой поверхности, то в автомодельной области можно производить исследование нагревания аппаратов на образцах уменьшенных размеров и при меньших токах. При этом надо помнить, что условие Сr-Рr>2· 10+7 должно быть выполнено и для уменьшенного образца. Можно рассчитать, что при этом определяющий размер модели должен быть не меньше 17 см, а ток в модели должен удовлетворять равенству

где индекс «о» относится к оригиналу, а индекс «м» — к модели; k — коэффициенты поверхностного эффекта.

§ 11.12. НАГРЕВАНИЕ НЕТОКОВЕДУЩИХ ЧАСТЕЙ АППАРАТОВ

Нагревание нетоковедущих частей аппаратов (за исключением частей из ферромагнитных материалов) происходит за счет теплопроводности и излучения от токоведущих частей. Части из ферромагнитных материалов нагреваются за счет поверхностного эффекта, создаваемого в них переменным магнитным полем токоведущих частей.
Анализ вопроса показывает, что потери на гистерезис и вихревые токи в ферромагнитном теле определяются не его сечением, а его периметром. Расчеты Л. Р. Неймана [Л. II.2] показали, что мощность потерь в ферромагнитном теле от гистерезиса и вихревых токов при резком проявлении поверхностного эффекта выражается простой формулой
(11.64)

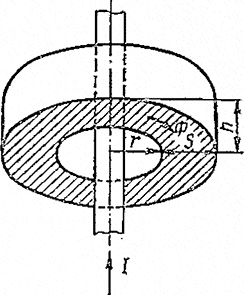
Рис. 11.8. Ферромагнитный тороид, по оси которого проходит токоведущий проводник
где Нe— действующее значение касательной, составляющей напряженности магнитного поля на поверхности ферромагнитного тела в данной точке поверхности; ω—угловая частота; μ— магнитная проницаемость материала тела при Н=Не по основной кривой намагничивания; у — удельная электропроводность материала.
Условия резкого проявления поверхностного эффекта, при которых возможно пользование формулой (11.64), соблюдаются при частоте 50 гц для всего сортамента фасонной стали. Возникает вопрос, как определить величину Не для различных ферромагнитных конструкций. Остановимся на одном частном случае, представляющем интерес в области электроаппаратостроения.
Предположим, что ферромагнитное тело представляет собой тороид, по оси которого проходит токоведущий проводник (рис. II.8). Этот рисунок схематически представляет фланец ввода в масляный выключатель. Допустим, что ток, текущий в проводнике, достаточно велик и создает на внутренней поверхности тороида высокую напряженность магнитного поля НСт. Глубина проникновения волны магнитного поля в тороид весьма мала по сравнению с толщиной s тороида, поэтому волну можно рассматривать как плоскую. Пользуясь уравнениями Максвелла, можно получить следующие зависимости:
(11.65)
Трудность интегрирования уравнений (11.65) заключается в том, что μ представляет собой сложную функцию от Нт. Однако при некоторых вполне приемлемых допущениях [Л. II.2] уравнения (11.65) возможно проинтегрировать и найти выражение для активного сопротивления R тороида:

— магнитная проницаемость материала тороида, определенная по основной кривой намагничивания при Я = Нт.
Мощность потерь в тороиде определяется равенством
(11.66)
Преобразуем это равенство:
(11.67)
Мощность на единицу внутренней поверхности тороида
(П.68)
Для расчета мощности по формуле (11.68) необходимо знать зависимость магнитной проницаемости μ0 от напряженности магнитного поля. Эти зависимости для чугуна и мягкой стали, нередко применяемых в аппаратуре, приведены на рис. II.9. Заметим, что на этом рисунке по оси абсцисс отложена амплитуда напряженности поля Нт, тогда как в уравнение (11.68) входит действующее значение Не. Можно принять, что на поверхности тороида напряженность поля является синусоидальной функцией. Тогда ,
На рис. 11.10 даны графики зависимости P/F = f(Н), вычисленные по формуле (11.68). Они удовлетворительно сходятся с опытными данными.
Расчеты показывают, что мощность, выделяющаяся в чугунных фланцах вводов в выключатели, даже при умеренных номинальных токах весьма велика и отвести ее в окружающую среду без специальных мероприятий невозможно. С этим затруднением можно справиться несколькими способами:

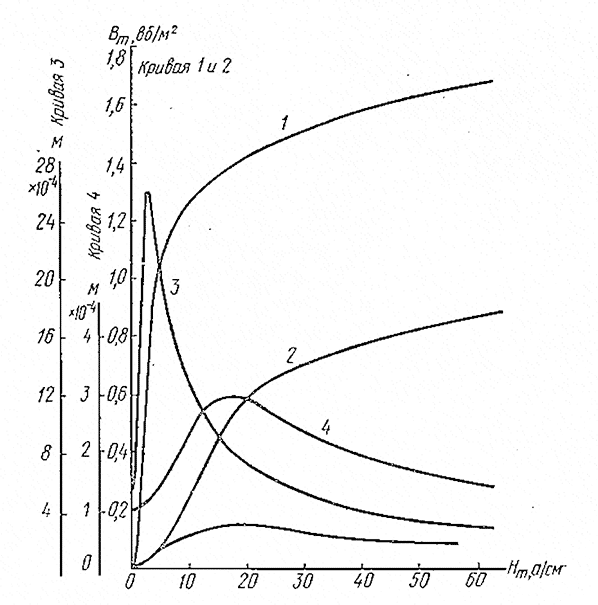
Рис. II.9. Зависимость от напряженности магнитного поля:
индукции: 1— для мягкой стали; 2 —для чугуна: магнитной проницаемости: 3 — для мягкой стали; 4 — для чугуна

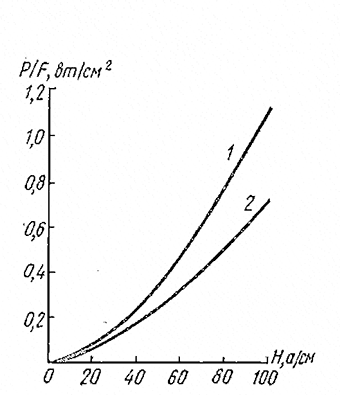
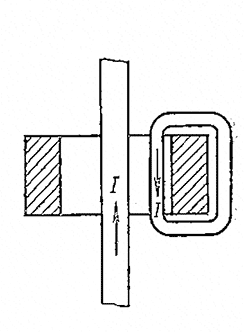
Рис. 11.11. Короткозамкнутый виток, наложенный на тороид
Рис. 11.10. Зависимость удельных потерь в тороиде из мягкой стали (1) и чугуна (2) по формуле (11.68)

1. Возможно применение немагнитных материалов вместо ферромагнитных, например, немагнитного чугуна, латуни, бронзы и т. п. Этот способ дорог и им можно пользоваться, когда соответствующие конструктивные элементы невелики и их стоимость не отражается заметно на стоимости аппарата.
2. Устройство прорезов в тороидальной конструкции, что включает воздушные (или вообще немагнитные) промежутки на пути магнитного потока и уменьшает этот поток, а следовательно, уменьшает индукцию в материале конструкции; в результате уменьшаются и потери в конструкции. Такой способ находит применение в практике аппаратостроения, так как он легко выполняется конструктивно. Чтобы прорез не ослаблял механическую прочность конструкции, его заливают латунью. Точный расчет влияния прореза затруднителен. Обычно идут по методу подбора, проверяя данные приближенного расчета опытом.        
3. Применение короткозамкнутых витков. Предположим, что на тороид наложен короткозамкнутый виток, как показано на рис. 11.11. Эта конструкция аналогична трансформатору тока с короткозамкнутой вторичной обмоткой, поэтому легко поддается расчету. Результирующий магнитный поток в таком устройстве мал, а потому малы и потери в тороиде. Однако взамен потерь в ферромагнитном материале появляются потери в короткозамкнутом витке. Задавая сечение витка, найдем его сопротивление R0 и потери в нем Рв= IRB.

Если предположить, что выделяющиеся в короткозамкнутом витке потери должны быть отведены непосредственно с его поверхности, то эта поверхность должна иметь очень большие размеры. Но эти потери отводятся не только через его собственную поверхность, но и через поверхность связанного с ним тороида (фланца ввода), поэтому необходимо осуществлять возможно более тесный контакт витка с фланцем. Расчет и опыт показывают, что применение короткозамкнутого витка дает наилучший эффект.