В электрических аппаратах приходится иметь дело с нагреванием не только проводов и подобных им токоведущих систем, но и катушек (например, катушек электромагнитов, реле и т. п.). Процесс нагревания катушек представляет собой сложное явление в силу того,что тепло, выделяющееся в витках, должно пройти длинный и зачастую извилистый путь через изоляцию и соседние витки, прежде чем будет отдано с поверхности катушки в окружающую среду. Точный расчет этого процесса, являющийся трехмерной задачей, связан с очень большими трудностями и производится обычно приближенно. Чтобы выяснить в общих чертах характер явления, можно сделать некоторые допущения, не приводящие, как показывает опыт, к значительным расхождениям с действительностью.
Первое приближение в решении этой задачи — определение средней температуры катушки по выделяющейся в ней мощности и среднему коэффициенту теплоотвода с ее поверхности в окружающую среду. Температура по сечению катушки распределяется неравномерно, выяснить закономерность ее распределения этот расчет не позволяет.

Рис. 11.21. Продольное сечение катушки
Рассмотрим второе приближение в решении этой задачи. Пусть имеется катушка, сечение которой представлено на рис. 11.21. Сечение катушки может быть в плане как круглым, так и прямоугольным. Для простоты рассмотрим круглую катушку. Сделаем следующие допущения:
- тепло выделяется равномерно по всему сечению катушки;
- материал сечения обладает некоторым средним коэффициентом теплопроводности, зависящим от сечения проводников, толщины их изоляции и взаимного расположения проводников (на определении среднего или эквивалентного коэффициента теплопроводности остановимся далее); ‘
- катушка может быть пропитана компаундом или не иметь пропитки; практически катушки электрических аппаратов всегда пропитываются компаундом, и этот случай мы в дальнейшем будем иметь в виду;
- торцы катушки имеют хорошую тепловую изоляцию, так что в этом случае теплоотводом через них можно пренебречь и считать, что тепло выделяется только через боковые поверхности катушки (радиальный теплоотвод);
- в уравнении теплопроводности не будем учитывать зависимость сопротивления от температуры и введем в расчет удельное сопротивление обмотки при средней температуре нагретой катушки, которое может быть определено по первому приближению.
Тогда уравнение теплопроводности можно написать в следующем виде: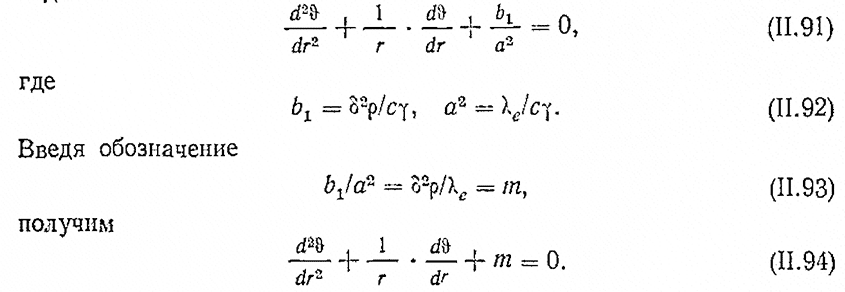
Решая эти уравнения, получим

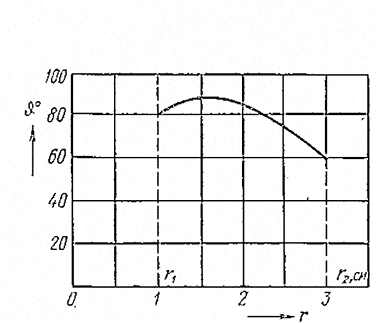
Рис. 11.22. Распределение температуры вдоль радиуса катушки
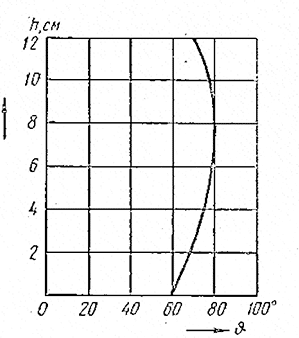
Рис. 11.23. Распределение температуры по высоте катушки
Пользуясь выведенными формулами, можно вычислить распределение температуры по радиусу катушки. Результаты этого вычисления приведены на рис. 11.22. Из рисунка видно, что максимум температуры достигается на некотором расстоянии от внутренней полости катушки. Этот максимум значительно превосходит температуру на наружной поверхности.
Могут быть условия, когда k2> kt (например, при наличии стального сердечника, плотно входящего во внутреннюю полость катушки). В этом случае максимум температуры может быть ближе к наружной поверхности катушки.
Допущение о полной тепловой изоляции торцов катушки не всегда справедливо. Некоторое количество тепла может отводиться через торцы катушки, и распределение температуры по длине ее может оказаться неравномерным. Типичное распределение температуры по длине катушки показано на рис. 11.23. Обычно нижний торец катушки охлаждается лучше, чем верхний, поэтому его температура ниже, чем температура верхнего торца. Однако если катушка расположена горизонтально, то температура обоих торцов может быть одинакова.
Остановимся на определении средней или эквивалентной теплопроводности обмотки катушки. Рассмотрим два случая: сечение проводников прямоугольное и сечение проводников круглое. Пусть тепловой поток направлен перпендикулярно к длинной стороне прямоугольника (рис. 11.24). Тогда эквивалентная теплопроводность
![]() (11.108)
(11.108)
где λ— коэффициент теплопроводности изоляции.
Если тепловой поток направлен перпендикулярно к короткой стороне прямоугольника, то
![]()
(11.109)
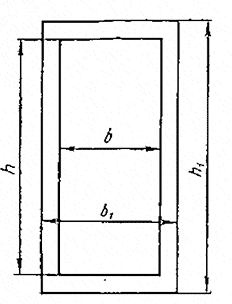
Рис/ 11.24. Сечение плоского проводника катушки
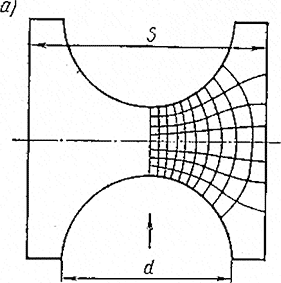
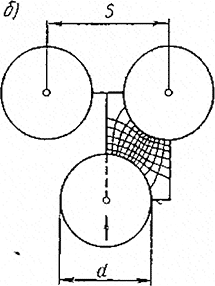
Рис. 11.25. Тепловое поле между круглыми проводниками катушки:
а — параллельное расположение проводов; б — треугольное расположение проводов
Таким образом, задача решается очень просто. Заметим, что в данном расчете мы считаем теплопроводность меди весьма большой по сравнению с теплопроводностью изоляции.
В случае круглых проводов задачу можно решить, построив тепловое поле между ними. Такое построение было выполнено Г. Н. Петровым [Л. 11.9]. Результаты его представлены на рис. 11.25. Произведя ряд расчетов для разных значений β = 2∆/d, где Δ — толщина изоляции и d—диаметр провода, Г. Н. Петров получил зависимость, которую можно выразить следующими эмпирическими формулами:
а) параллельное расположение проводов
![]() (11.110)
(11.110)
б) треугольное расположение —
![]() (11.111)
(11.111)
Опытное определение этих зависимостей [Л. 111,10] привело к следующим формулам:
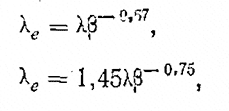
(11.112)
(11.113)
где принято β= ∆|d.
Расхождение с теоретическими формулами невелико.


