Оценка ресурса, его продление и увеличение межремонтного периода являются важными для современного энергетического оборудования в нашей стране и за рубежом. Актуальность проблемы предельного ресурса энергетического оборудования обусловлена прежде всего неуклонным возрастанием доли оборудования, отработавшего расчетный или назначенный срок службы. Динамика роста удельного веса тепломеханического оборудования на АЭС и ТЭС, отработавшего назначенный ресурс, в нашей стране и за рубежом практически одинакова. Так, в США на долю оборудования, отработавшего свыше 30 лет, в 1970 г. приходилось только 1,5% установленной мощности, в то время как в 1990 г. эта величина достигла 15%. Предполагается, что к 2000 году долю оборудования, отработавшего назначенный ресурс 25-30 лет, может составить 25-35% общего объема установленных мощностей. Учитывая малые резервы энергетических мощностей в нашей стране и значительные ежегодные наработки оборудования, обеспечение достаточной надежности и стабильности выработки тепловой и электрической энергии при требуемой безопасности потребует больших затрат и усилий многих коллективов конструкторов, ученых и эксплуатационников. Важнейшая задача при определении ресурса - это правильное выявление связи ресурса с безотказностью, безопасностью и экономической эффективностью. При любой системе установления ресурса должны быть обоснованы прежде всего предельно допустимые значения наработки оборудования, важного для безопасности. Первоначальной основой для оценки ограничений ресурса является расчетная долговечность оборудования. В расчетных методах оценки долговечности исходят из предположения, что долговечность ограничивается усталостными свойствами, следовательно, речь идет о прочностном ресурсе оборудования.
Метод линейного суммирования повреждений широко используется при расчете прочностного ресурса оборудования и сооружений АЭС. Этот метод основывается на следующей гипотезе: усталостное повреждение объекта является линейной функцией числа циклов нагружения:
(4.4)
где п - число уровней циклов нагружения оборудования, различных по амплитуде; Niф - фактическое число циклов нагружения оборудования, определенной амплитуды; [N]i - число циклов нагружения
той же амплитуды, необходимое для разрушение объекта. Из выражения (4.4) следует, что разрушение объекта происходит тогда, когда сумма всех " удельных" (относительных) повреждений будет равна единице.
Вероятность разрушения в общем случае равна
Рис. 4.5. Схема суммирования повреждений:
- - линейный закон накопления усталостных повреждений; 2 - фактическое накопление усталостных повреждений.
(4.5)
Схема суммирования повреждений представлена на рис. 4.5 Ломаная линия Ок означает задаваемый при расчетах закон накопления повреждений объекта. Фактический процесс накопления усталостных повреждений в объекте изображен на рис. 4.5 линией Оабс. Из приведенных зависимостей (4.4) и (4.5) и кривых рис. 4.5 следует, что вероятность неразрушения объекта P(N) = 1 — Q(N) = = 0,5, задаваемая по закону накопления повреждений Qk , может соответствовать истинной вероятности неразрушения по закону Qaбс значительно более высокой, например, порядка 0,999. Однако, учитывая сложность конструкций оборудования энергоблока АЭС, а также условия их нагружения в процессе эксплуатации, полученная таким образом вероятность неразрушения (0,999) является недостаточной для исключения появления трещин в элементах конструкции оборудования.
К недостаткам методик, основанных на методе механики линейного суммирования, относятся следующие:
процессы трещинообразования в элементах конструкций тепломеханического оборудования энергоблока АЭС, связанные с такими явлениями, как коррозия, тепловое старение, износ, эрозия, флюенс нейтронов, влияние которых имеет существенно нелинейный характер;
циклы нагрузки во времени эксплуатации оборудования, которые могут распределяться неравномерно и иметь различную интенсивность, что может совершенно исказить линейную модель.
Методы механики разрушения используют аналитические зависимости, связывающие время до разрушения конструкционного элемента оборудования с параметрами физико-химических процессов в материалах и характеристиками материала и нагружения. Так, формула С.Н.Журкова дает связь между напряжением, температурой и временем от момента приложения механической нагрузки до разрушения материала образца при растяжении:
где tpo - постоянная величина, приблизительно равная периоду тепловых колебаний атомов в твердом теле (10-12с); Еа - энергия активации процесса разрушения; к ~ 1,38 - 10-23 Дж/К - постоянная Больцмана; U0 - энергия, близкая к энергии сублимации материала; V - активационный объем материала.
Если на всех стадиях разрушения материала ведущим процессом является пластическая деформация, то время до разрушения равно
(4.7)
где Еср - средняя скорость пластической деформации; бР - максимальное относительное удлинение образца. Ползучесть как процесс медленного пластического течения металлов во времени обычно описывается показательным законом
(4.8)
где ё - скорость ползучести; с - коэффициент; R1 - универсальная газовая постоянная.
Для реакторных материалов, работающих в условиях изменяющихся напряжений и температур, деформация и время разрушения связаны соотношением:
(4.9)
где tp и ер - соответственно время и деформация при разрушении; emin - минимальная скорость ползучести; К и а - постоянные.
Развитие физики твердого тела, металловедения и механики разрушения привело к дислокационным моделям развития и распространения трещин. Рост трещин в твердых телах описывается соотношением Пэриса:
(4.10)
где 2 - длина трещины; N - число циклов нагружения; АК - размах коэффициента интенсивности напряжений (КИН); А - постоянная материала; п - параметр материала, зависящий от симметрии нагружения и направления роста трещины (п = 2 6). Имеется большое число работ, где время до разрушения объекта в условиях трещинообразования определяется из уравнения Пэриса, в котором рост трещины за цикл нагрузки является функцией фактора КИН.
Большое число повреждений металла тепломеханического оборудования происходит вследствие трещинообразования под влиянием коррозии в среде теплоносителя. Основными ведущими механизмами докритического роста трещин являются следующие процессы:
химическая коррозия под напряжением; электрохимическая коррозия под напряжением; водородное охрупчивание; коррозия под облучением.
Если скорость коррозионной трещины представляет собой некоторый функционал во времени от КИН
(4.11)
где р - давление теплоносителя, и если выполняются условия тонкой структуры пленки и гипотезы локальности разрушения металла в вершине трещины, то время до разрушения объекта можно записать в виде
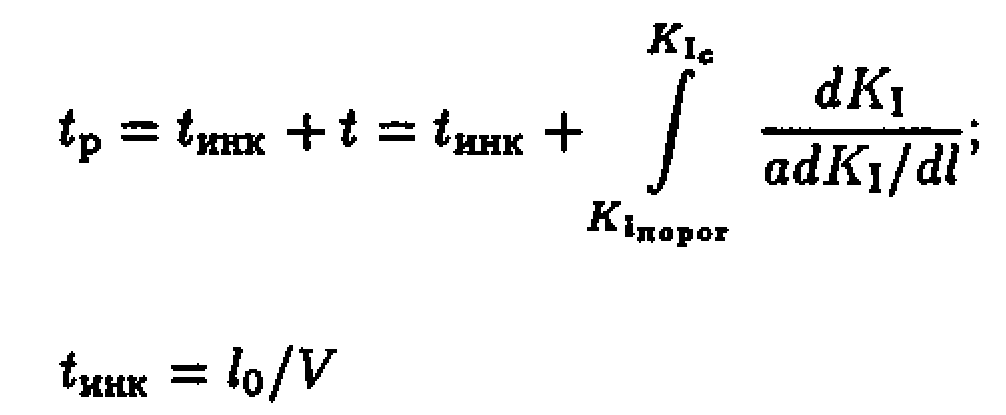(4.12)
- инкубационный период роста трещины, составляющий 70-80% времени до разрушения; V - скорость роста трещины; Iq - начальный размер трещины;
(4.13)
- время критического роста трещины; К1с - критическое значение КИН у вершины трещины; пороговое значение КИН, ниже которого подкритический рост трещин отсутствует, эквивалентное напряжение, а - коэффициент; для случая химической коррозии
к1 - константа скорости химической реакции на границе раздела коррозионная пленка-металл; Д0 - коэффициент диффузии наиболее активного компонента.
Методы параметрического прогнозирования ресурса. Методологической базой решения проблемы надежности машин и систем вообще и проблемы ресурса в частности, является разработка методов прогноза возможных изменений в элементе, оборудовании, системе, машины в целом на основе изучения физики процессов старения с их стохастической природой. Надежность объектов часто понимается примитивно как отказ их функционирования, поломка, заклинивание, течь, невыполнение управляющих сигналов, работа на недопустимых режимах и т.д.
Рис. 4.6. Схема изменения состояний объекта
Такие отказы возникают, как правило, из-за нарушений условий эксплуатации, при допущении ошибок при проектировании и изготовлении оборудования. Этого в большинстве случаев удается избежать за счет ужесточения организационно-технических мероприятий, высокой культуры производства, контроля и эксплуатации. Внутренние же изменения, присущие любой сложной системе, подчинены иным законам, они медленно, но неизбежно изменяют характеристики оборудования, его выходные параметры, в том числе и ресурсные.
Имеются три основных источника воздействий на объект: действие энергии окружающей среды, включая человека, исполняющего функции оператора, эксплуатационника и ремонтника;
внутренние источники энергии, связанные с рабочими процессами, протекающими в объекте;
потенциальная энергия, накопленная в материалах конструкции объекта в процессе изготовления и эксплуатации.
Эти формы энергии, действуя на объекты, вызывают в них процессы, ухудшающие начальные параметры объектов, т.е. могут привести к отказу (рис. 4.6).
Рассмотрим общую схему формирования параметрического (постепенного) отказа (рис. 4.7).
Пусть протекание различных процессов повреждения в материалах N однотипных объектов приводит к изменению во времени t выходных (ресурсных) параметров (на рис. 4.7 в качестве примера показан возрастающий характер изменения. Отказ объекта наступает при достижении его параметром своего допустимого значения. В начальный момент времени эксплуатации объекта t = 0 имеет место разброс параметра относительно своего математического ожидания. Если выборка объектов значительна по объему, то при отказе всех N объектов можно построить плотность распределения наработки и вычислить значение среднего ресурса Тр . Значение t =А характеризует зону безотказности объекта, а заштрихованная область ЗН - запас надежности. Изменение параметра У(t) в процессе эксплуатации является случайным и зависит от скорости v(t, У) = dV/dt изменения повреждений отдельных элементов объекта. В результате в каждый момент времени ti , i = 0,1,2,..., происходит формирование закона распределения, который определяет вероятность выхода параметра У за границу Удоп. При У = Удоп наступает предельное состояние объекта.
