Под идентификацией будем понимать процедуру построения оптимальной (в определенном смысле) математической модели объекта по реализациям его входных и выходных сигналов. Одной из важных задач, решаемых идентификацией, является определение характеристик динамических систем ЯЭУ. Когда математическая модель объекта контроля известна с точностью до параметров, а задачей идентификации является их количественная оценка, последняя решается методами параметрической идентификации. В идентификации используются методы теории вероятностей, математической статистики, математической логики, теории автоматического управления, теории распознавания образов и т.д.
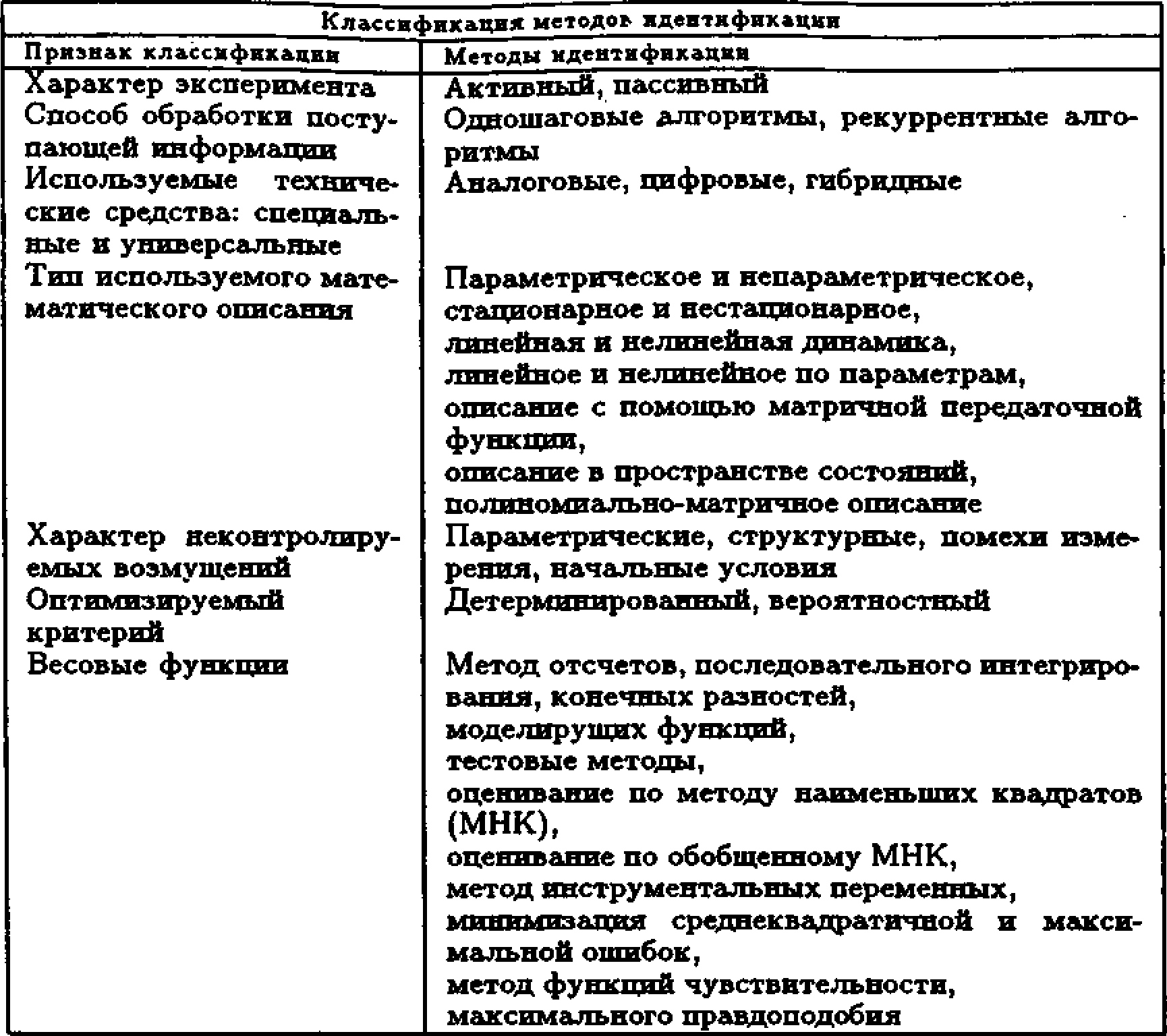
Классификация методов идентификации может быть осуществлена различными способами. В табл. 19.2 приведены основные принципы классификации методов идентификации.
В зависимости от способа получения экспериментального материала различают пассивный и активный эксперимент идентификации.
Оценивание параметров математического описания состояния оборудования ядерной энергетической установки в режиме нормального функционирования составляет суть пассивного эксперимента. Активный эксперимент предполагает изменение режимов функционирования оборудования ядерной энергетической установки по специальному плану. Хотя активный эксперимент позволяет более эффективно решать задачи идентификации, однако он не всегда выполним в силу особенностей функционирования реальной ЯЭУ. Для некоторых элементов оборудования ядерной энергетической установки, например, блоков СУЗ, системы контроля нейтронного потока и т.п. при активном эксперименте на вход исследуемого объекта подаются специальные тестовые сигналы: импульсные, синусоидальные. Для поиска эффективного входного сигнала привлекаются методы оптимального планирования эксперимента.
По способам обработки поступающей информации в методах идентификации используются два принципа: одношаговые и рекуррентные алгоритмы. Оценивание параметров моделей объекта в одношаговых алгоритмах идентификации осуществляется после предварительного накопления реализаций входного и выходного сигналов (алгоритмы "off-line").
Преимуществом одношаговых алгоритмов является высокая точность получения оценок параметров, а недостатком - потребность в запоминающих устройствах или в записывающей аппаратуре.
Рекуррентные (многошаговые) алгоритмы идентификации позволяют оценивать параметры после каждого нового измерения наблюдаемых сигналов (алгоритмы " online"). Такие алгоритмы обработки данных снижают требования к запоминающим устройствам и позволяют не решать заново систему алгебраических уравнений относительно оцениваемых параметров, что очень важно при большой размерности задачи.
Области применения одношаговых и рекуррентных алгоритмов: одношаговые алгоритмы используются большей частью для однократного оценивания параметров объекта после поступления всех измерений входного и выходного сигналов, а рекуррентные - для оценивания параметров "в темпе процесса".
Решение задач идентификации оборудования ядерной энергетической установки требует значительных вычислительных затрат. Так как задачи идентификации разнообразны, то и применяемые средства вычислительной техники различны. Реализация задачи идентификации в режиме "off-line", т.е. с предварительным накоплением данных, связана с получением результатов после окончания эксперимента идентификации и в большинстве случаев эта задача решается на универсальных ЭВМ. Это объясняется тем, что универсальные ЭВМ обладают большими возможностями запоминания массивов информации. При оценивании параметров объекта и использовании получаемых результатов, например для функционального диагностирования в процессе функционирования реального объекта, основное значение имеет скорость выполнения малого числа вычислительных процедур, характерных для конкретной задачи. Использование рекуррентных алгоритмов (в режиме "on-line") уменьшает объем необходимой оперативной памяти ЭВМ. Поэтому таким требованиям наилучшим образом удовлетворяют специализированные ЭВМ. Набор средств для реализации вычислительного процесса идентификации может содержать цифровые, аналоговые и гибридные ЭВМ. В современных условиях все большее применение получает гибридная вычислительная техника, позволяющая сочетать преимущества аналогового и цифрового способов обработки информации.
Наиболее многочисленная классификация методов идентификации имеет место по виду математической модели. В качестве математической модели идентифицируемого объекта используют различные формальные описания, которые могут быть разделены на два больших класса: параметрические непараметрические. В первом случае задача идентификации сводится к оцениванию конечного числа параметров, являющихся, как правило, коэффициентами алгебраических, дифференциальных, интегральных или разностных уравнений. Преимущество такого описания заключается в конечности числа оцениваемых параметров, а недостаток - в трудностях определения порядка (структуры) используемого уравнения. При непараметрическом описании характеристиками объекта теоретически будет бесконечно большое (на практике достаточно большое) число параметров. Примеры таких моделей: импульсные и переходные функции объектов, частотные характеристики. Положительной стороной непараметрического описания является отсутствие задачи определения структуры модели объекта, недостатками - очень большое число оцениваемых параметров и трудности при использовании таких моделей.
Поскольку для большинства элементов основного оборудования ядерной энергетической установки структура математического описания предполагается известной априори, то для идентификации наиболее удобно использовать параметрические модели. Среди таких моделей могут быть модели с постоянными и переменными параметрами, с линейной и нелинейной динамикой.
Если параметры объекта не изменяются во времени (стационарный случай), то задача оценивания коэффициентов модели относительно проста и осложняется, в основном, только помехами измерения. Оценивание дрейфующих параметров (нестационарный случай) связано с наличием параметрических возмущений, которые могут быть либо известными заранее, либо случайными. В первом случае закон изменения параметров, как правило, задается и остается определить постоянные коэффициенты этого закона. Во втором случае задача усложняется: изменение параметров модели объектов во времени зависит от изменения как режимных параметров ЯЭУ (мощности, температуры, расхода и давления теплоносителя), так и ряда других эксплуатационных факторов (вибраций, химического состава теплоносителя, облучения и т.п.). Суммарный результат воздействия комплекса таких факторов во времени описывается моделями случайных процессов (как правило, нестационарных), так как аналитический расчет влияния такого множества факторов практически невозможен.
Для задачи оценивания параметров математической модели объекта существенное значение имеет линейность параметров относительно свободной переменной. Использование таких моделей сводит задачу оценивания параметров к решению системы линейных алгебраических уравнений. Оценивание параметров уравнений для объектов с линейной и нелинейной динамикой принципиальных отличий не содержит. Также мало отличаются методы идентификации объектов, описываемых уравнениями с дискретным временем от методов идентификации объектов, представляемых моделями с непрерывным временем.
Среди видов математического описания динамических объектов широкое распространение получили описания с помощью дифференциальных уравнений, передаточных функций, описание в пространстве состояний и полиномиально-матричное описание.
Классификация по характеру неконтролируемых возмущений.
Определение оценок параметров математического описания динамических объектов существенно усложняется тем, что в процессе эксплуатации на объект контроля постоянно воздействуют различного рода возмущения, среди которых следует выделить полезные и вредные. Вредные или неконтролируемые возмущения можно классифицировать следующим образом:
помехи, непосредственно влияющие на наблюдения входного и выходного сигналов объекта;
параметрические возмущения, воздействующие на наблюдаемые сигналы косвенно через измерения параметров объекта;
структурные возмущения, изменяющие структуру объекта идентификации;
неучтенный запас собственной энергии объекта (неизвестные начальные условия).
Источником первой группы возмущений является прежде всего зашумленность каналов наблюдения входного и выходного сигналов. Параметрические возмущения обусловлены постепенной потерей требуемых свойств конструкционных материалов в процессе эксплуатации (коррозия, старение, эрозия и т.п. процессы). Эти возмущения воздействуют на выходной сигнал косвенно, через функции чувствительности. Структурные возмущения появляются из-за того, что при выборе структуры модели для описания очень сложных объектов отбрасываются малосущественные факторы и связи при декомпозиции модели.
Специфика проблемы идентификации оборудования ядерной энергетической установки как сложных систем.
Особенности оборудования ядерной энергетической установки накладывают определенные закономерности на решение проблемы идентификации. К этим специфическим особенностям можно отнести следующее.
- Большинство элементов оборудования ядерной энергетической установки является динамическими объектами. Идентификация динамических объектов дает хорошие результаты при использовании методов активного эксперимента путем формирования специальных тестовых входных сигналов. Как правило, входные тестирующие сигналы могут приниматься заданными и их измерение при активной идентификации не является обязательным. При невозможности осуществления активной идентификации используют методы пассивного эксперимента с помощью методов регрессионного и корреляционного анализа.
- Основная трудность при решении задачи идентификации связана с тем, что выходные сигналы динамического объекта, а также сигналы устройств измерения искажены случайными помехами. Таким образом, измеряемые сигналы всегда следует считать случайными, и идентификация оказывается тесно связанной с фильтрацией случайных помех. Алгоритмы идентификации должны обеспечивать наилучшую (в статистическом смысле) точность оценки неизвестных параметров и (или) характеристик динамического объекта и в наибольшей степени ослабить влияние случайных помех. Специфика идентификации заключается в том, что требуется не просто отделить полезный сигнал от шумов, а оценить параметры этого сигнала, являющегося одновременно параметрами динамического объекта.
- Динамический характер объектов ЯЭУ приводит к тому, что параметры объектов, во-первых, дрейфуют, во-вторых, практически очень трудно провести повторные, дублирующие измерения из-за невозможности перевода объекта идентификации в исходное начальное состояние, и в-третьих, необходимо идентифицировать некоторые непосредственно не измеряемые характеристики, погрешность которых может задаваться в виде интегрального функционала.
- Процесс идентификации осложняется наличием нелинейных элементов в системах ЯЭУ. Это ограничивает амплитуду тестирующих воздействий, которые должны быть определены так, чтобы при уменьшении их амплитуды форма переходных процессов на выходах системы не менялась. Для идентификации частотных характеристик обычно используются периодические (гармонические) сигналы, но это требует длительных экспериментов большого объема, так как необходимо ожидание конца переходных процессов. В этом плане большие преимущества дает использование при идентификации динамических объектов непериодических тестирующих входных сигналов, обеспечивающих минимум интервала наблюдения при заданном значении показателя точности идентификации.
- Нетрудно убедиться, что алгоритмы идентификации оказываются более сложными, чем алгоритмы функционирования контролируемого объекта ЯЭУ. Даже для одномерных стационарных детерминированных динамических объектов системы идентификации их параметров оказываются многомерными, нестационарными, часто нелинейными и случайными. Случайность проявляется в том, что результаты измерений искажены случайными сигналами. Типичными нелинейными элементами системы индикации являются блоки перемножения в той или иной форме. Переменные коэффициенты появляются в нестационарных фильтрах, выделяющих оценки параметров. Многомерность возникает из-за необходимости оценки не одного, а нескольких неизвестных коэффициентов. При оценке параметров многомерных систем алгоритм идентификации оказывается матричным или многомерно-матричным. Отсюда видно, что размерность матриц, используемых при идентификации, возрастает по сравнению с размерностью матриц, описывающих объект контроля.


