7-16. Согласование нагрузки в эквивалентной схеме
В главе, посвященной «языку электротехники», много внимания было уделено Т-образной схеме — схеме замещения любого канала передачи электрической энергии (рис. 7-10). Эта схема — важный объект экстремальных исследований.
Одна группа задач формулируется таким образом. Заданы величины всех трех сопротивлений в схеме замещения. Надо подобрать сопротивление нагрузки (сопротивление приемной цепи). Можно подобрать это сопротивление, исходя из самых различных заданий, но чаще всего «наилучшее» сопротивление нагрузки должно соответствовать либо наибольшей мощности, получаемой во вторичной цепи, либо наименьшим потерям энергии при ее передаче (наибольшему к. п. д.).

Рис. 7-11. По оси ординат — отношение теряемой при передаче энергии к полезной энергии на нагрузке. По оси абсцисс — отношение сопротивления связи к среднему геометрическому сопротивлению в первичной и вторичной цепях в эквивалентной Т-образной схеме замещения. Сопротивление нагрузки подобрано оптимальное.
Когда сопротивление нагрузки равно бесконечности — это режим холостого хода, полезная мощность на нагрузке равна нулю, в системе существуют только потери, и к. п. д. передачи также равен нулю.
Когда сопротивление нагрузки равно нулю — это режим короткого замыкания, полезная мощность на нагрузке также равна нулю и к. п. д. равен нулю, ибо в системе при этом также существуют только потери.
Существует определенная величина сопротивления нагрузки, при которой к. п. д. получается наибольшим, потери — наименьшими.
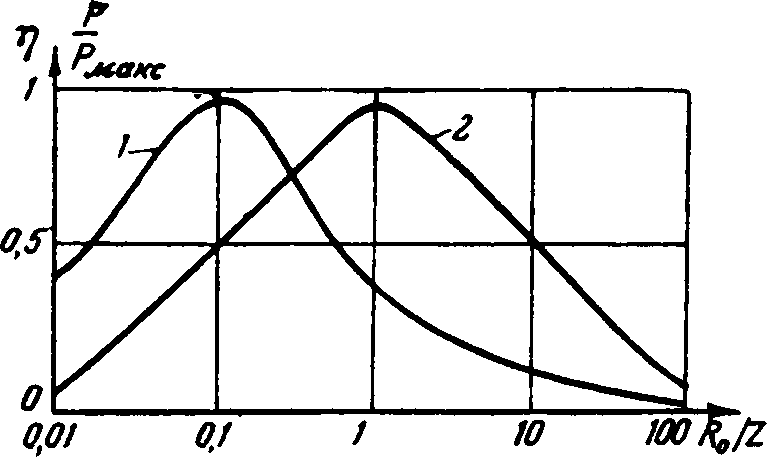
Рис. 7-12. Полезная мощность на нагрузке (кривая 1) и к. п. д. передачи (кривая 2) в сильноточном канале в зависимости от величины отношения сопротивления нагрузки R0 к сопротивлению связи Z.
На рис. 7-11 показано, как меняется отношение потерь в первичной цепи Р1 и во вторичной цепи Р2 к полезной передаваемой мощности P0 в зависимости от отношения сопротивления связи к сопротивлению потерь.
На рис. 7-11 вверху показаны индуктивно связанные контуры, но кривые этого рисунка могут быть справедливы и для схемы рис. 7-10.
Здесь не к чему приводить точную формулу для определения сопротивления нагрузки, дающего наилучший к. п. д. Эта формула в общем виде громоздка и мало наглядна. Также громоздка и формула для вычисления сопротивления нагрузки, которое дает не наибольший к. п. д., а наибольшую полезную мощность на нагрузке. Важно только подчеркнуть, что для получения наивысшего к. п. д. нужно большее значение сопротивления нагрузки, чем для получения наибольшей мощности (рис. 7-12).
Расхождения этих «оптимальных» сопротивлений тем больше, чем выше максимально достижимый к. п. д. всей схемы передачи.
При очень плохом к. п. д. передачи, измеряемом процентами или даже долями процента, условия наибольшей мощности и наибольшего к. п. д. сближаются одно с другим (рис. 7-13). Оптимальное сопротивление нагрузки равно вредному сопротивлению потерь вторичного контура. Это случай передачи, когда в эквивалентной схеме замещения велики плечи и мала ножка.
В таких условиях обычно приходится работать слаботочникам, связистам. Часто они стремятся сделать свою нагрузку по сопротивлению равной сопротивлению потерь приемной цепи.
Когда активное сопротивление нагрузки равно активному сопротивлению приемного плеча эквивалентного Т, то это соответствует максимальной получаемой на нагрузке мощности. При больших плечах и малой ножке это условие совпадает и с оптимальным к. п. д. Это может быть очень жалкий, ничтожный к. п. д. — меньше одного процента, а бывает и меньше тысячной доли процента, но связисты часто довольствуются и таким к. п. д.
Сильноточники-энергетики, наоборот, применяют каналы передачи электроэнергии с к. п. д., как правило, большим 50%. Условия наименьших потерь при передаче выполняются при этом, когда в эквивалентной схеме активное сопротивление нагрузки равно сопротивлению связи в эквивалентном Т. При этом мощность, соответствующая максимальному к. п. д., т. е. получаемая при равенстве сопротивления нагрузки и сопротивления связи, может быть меньше 0,1 и даже меньше 0,01 от максимально достижимой на нагрузке мощности.
С уменьшением сопротивления нагрузки получаемая на ней мощность возрастает, но ухудшается к. п. д.
Часто случается, что сопротивление связи очень велико. В этих случаях его даже иногда принимают равным бесконечности и рисуют схему замещения канала передачи вовсе без ножки у буквы Т.
Оптимальный к. п. д. передачи при этом будет соответствовать очень малой передаваемой мощности. При этом оптимальном сопротивлении нагрузки невыгодно эксплуатировать канал передачи. Энергетики Нарочно идут на ухудшение к. п. д., так как этот ухудшенный к. п. д. еще достаточно высок. Для получения достаточно большой мощности берут сопротивление нагрузки, равное лишь нескольким долям от сопротивления связи.
В упрощенной схеме замещения канала передачи оптимальный к. п. д. соответствует сопротивлению нагрузки, равному бесконечности. Оптимальная мощность — это бесконечно малая мощность.
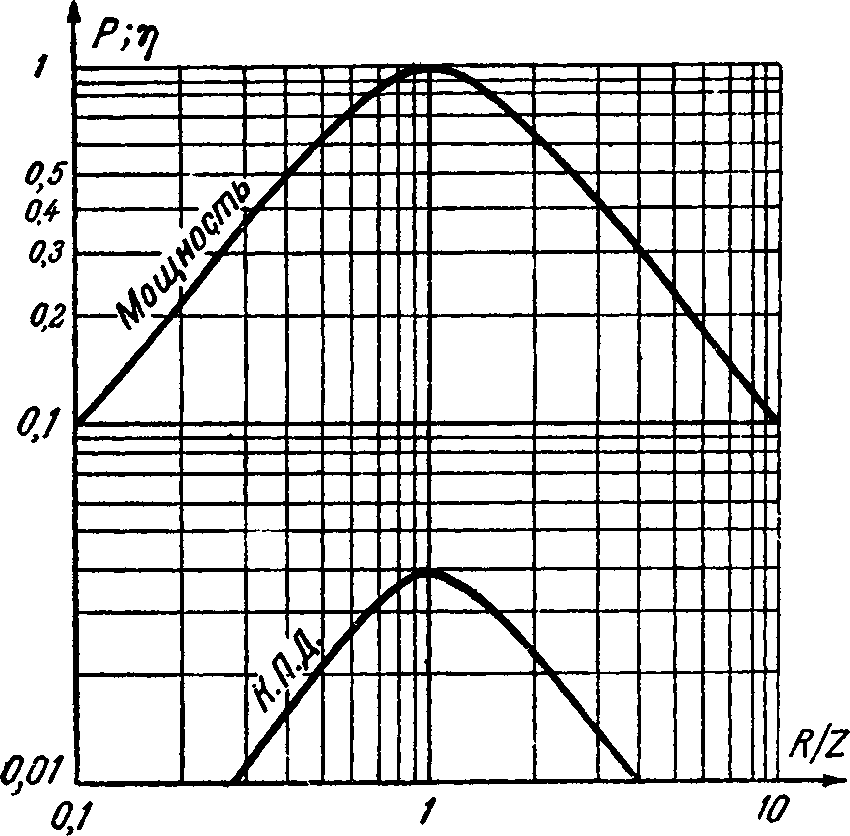
Рис. 7-13. Полезная мощность на нагрузке и к. п. д. передачи в слаботочном канале в зависимости от величины сопротивления нагрузки.
Наибольшая же мощность соответствует равенству сопротивления нагрузки полному сопротивлению цепи. Это старинное правило: сопротивление потребителя равно сопротивлению генератора.
Но приближение это очень грубое, им можно было довольствоваться лишь в те времена, когда генераторами были лишь гальванические элементы. В наши дни все значительно сложнее и тоньше.


