7-24. Плоскогорье вместо вершины
Бывает, что точка максимума выражена неотчетливо.
При индукционном нагреве в плавильной печи (фиг. 7-9), или для поверхностной закалки (о закалке будет рассказано в последующих разделах) важно получить высокий к. п. д. Переменный ток, циркулирующий в индукторе, создает вокруг его проводников быстропеременный электромагнитный поток. Этот поток пронизывает помещенное в индуктор изделие, возбуждает в изделии вихревые токи. Отношение мощности, выделяемой в изделии вихревыми токами, ко всей мощности, подводимой к индуктору, — это и есть интересующий нас электрический к. п. д. индуктора.
При низкой частоте тока в индукторе изделие, как уже говорилось, прозрачно для магнитного потока. Вихревые токи в изделии слабы, мощность, ими выделяемая, ничтожна по сравнению с потерями в индукторе. С повышением частоты тока в индукторе мощность в изделии растет сначала как квадрат частоты. Быстро растет к. п. д. Но затем рост к. п. д. замедляется. Вихревой ток в изделии не может быть интенсивнее, нежели породивший его ток индуктора. Коэффициент полезного действия приближается к некоторому предельному значению. Это предельное значение к. п. д. η0 зависит от сопротивления материала индуктора рi, сопротивления материала нагреваемого изделия ра и от соотношения поверхностей, омываемых быстропеременным магнитным потоком в индукторе Si. и изделии Sa.
Приближенно:![]()
Можно повысить частоту тока в 10 или даже в 100 раз, но к. п. д. никогда не достигнет значения η0. При еще большем повышении частоты к. п. д. может начать падать из-за того, что индуктор станет излучать электромагнитную энергию во все стороны, как антенна широковещательной радиостанции, и появятся большие потери в окружающих индуктор предметах. Но до этого предела обычно никогда не доходят по ряду других причин.
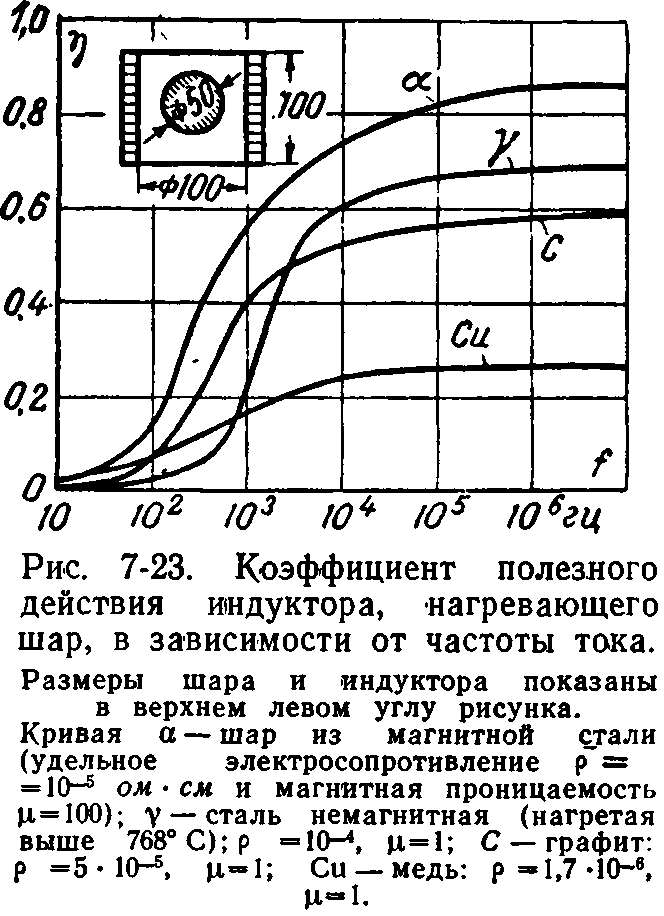
На рис. 7-23 представлен ход кривых к. п. д. для случая нагрева шаров диаметром 50 мм из разных материалов, помещаемых внутрь индуктора в виде цилиндрической спирали с высотой и диаметром, равными 100 мм.
Как здесь определить наивыгоднейшую частоту? Точки максимума на этих кривых нет. После крутого подъема идет перегиб, а затем почти горизонтальный участок.
Прежде всего надо указать, что нагревательный индуктор — это лишь одно звено установки высокочастотного нагрева. С индуктором всегда соединена (непосредственно или через трансформатор) конденсаторная батарея. И стоимость этой батареи, и потери в ней зависят от частоты. При одной и той же передаваемой полезной мощности затраты на батарею конденсаторов для разных частот могут отличаться в несколько раз.
От частоты тока зависит и тип генератора. Если частота тока выше 10 000 Гц, то целесообразно применять только генераторы с электронными лампами. Потери энергии в этих лампах могут превышать 20% от преобразуемой мощности. При более низких частотах можно применять и машинные генераторы, и генераторы с ионными лампами, в которых потери меньше 10%. Может оказаться выгодным несколько пожертвовать к. п. д. индуктора, но зато выиграть на к. п. д. генератора.
Можно построить кривую полного к. п. д. и полных эксплуатационных расходов нагревательной установки в зависимости от частоты тока. Но и эта кривая большей частью не имеет вида острого пика, а напоминает собой плоскогорье.
Но здесь электрик должен прислушаться к голосу металлурга и машиностроителя. При высокочастотном нагреве металлов энергетика — только служанка технологии. Основное назначение нагревательной установки — это не экономить энергию, а давать продукцию высшего качества. При поверхностной закалке часто приходится выбирать частоту, значительно более высокую, чем это нужно по соображениям к. п. д.
Так бывает при нагреве изделий сложной формы. Только высокочастотный ток может обойти по всем выступам и впадинам изделия. Иногда же, наоборот, выбирают явно заниженную с точки зрения электрика частоту, для того чтобы получить прогрев сразу в толстом слое и узкую переходную зону между нагретым и сердцевинным металлом.
Поэтому на кривой зависимости к. п. д. нагревательного индуктора от частоты тока надо иметь только какую-то опорную точку — точку, ниже которой к. п. д. растет быстро, а выше — медленно. Но это не такая определенная вещь, как точка максимума или минимума, которая определяется математически совершенно однозначно. Точка перехода от крутого склона к пологой части (колено на кривой)—это понятие условное.
В моей книге «Индукционный нагрев металлов» я так определил минимально допустимую частоту тока, или, что одно и то же, максимально допустимую длину волны:
«При нагреве цилиндра или шара из немагнитного материала надо, чтобы длина электромагнитной волны в этом цилиндре или шаре была меньше его радиуса. Коэффициент полезного действия сильно ухудшается, если ток имеет более низкую частоту и, следовательно, более длинную волну. При нагреве шара из магнитного материала колено кривой к. п. д. соответствует волне, которая в магнитную проницаемость (μ) раз меньше радиуса шара. Когда нагревается не шаровое и не цилиндрическое изделие, а плоская плита, то желательно, чтобы ширина индуктора была больше длины волны».
Разные авторы неоднократно предлагали иные формулировки для границы «достаточного электрического к. п. д.». Одни писали, что волна должна в полтора- два раза быть меньше радиуса нагреваемого цилиндра, а другие, наоборот, считали, что достаточно иметь волну, равную трем четвертям радиуса.
Мне приходилось слышать споры: «Ваш критерий неточен, а вот формула такого-то дает прекрасные результаты». Другие, наоборот, хвалили мое определение. Кто же прав? Да никто. Определение «достаточного электрического к. п. д.» — это не формула и не критерий, это скорее мнемоническое правило. Никакой особой точки на колене не существует.
Это правило только указывает, «быстро» или «медленно» растет к. п. д. на данном участке кривой. А конкретные значения этого к. п. д. надо получать полным расчетом.
И в других областях электротехники приходится сталкиваться с кривыми, не имеющими максимума. Кривая намагничивания стали идет сначала круто, а затем переходит в пологий участок. Где здесь точка насыщения? При каком значении индукции происходит перегиб в кривой? И здесь нельзя дать точного однозначного указания, а можно лишь отметить некоторую область магнитных индукций. Ниже нет насыщения, выше оно есть.
7-25. О катании с ледяных гор
Есть класс задач, которые исследованиями на максимум и минимум не решить. Для них требуются более тонкие вычисления. Необходимые методы были найдены математиками задолго до возникновения промышленной электротехники.
В 1696 г. в выдающемся научном журнале той эпохи «Акта Эрудиторум» была помещена следующая задача (мы приведем ее в несколько вольном изложении).
С вершины ледяной горы катятся санки. Гору надо считать идеально гладкой, и санки движутся по ней безо всякого трения, все ускоряясь по мере спуска. Заданы местоположения: вершины горы и некоторой точки у ее основания. Спрашивается: какое очертание должна иметь гора, чтобы санки, скатываясь с ее вершины, достигали основания в самое короткое время?
Легко понять, что время спуска сильно зависит от очертания горы. Если сделать спуск прямолинейным, то санки вначале будут разгоняться медленно. Ясно, что по прямому спуску санки скользнут не в самое короткое время. Если же, наоборот, сначала сделать спуск очень крутым, санки быстро разгонятся, но зато у основания горы санкам придется пройти длинный участок.
Ни дуги круга, ни другие элементарные кривые не давали решения задачи о санках, катящихся с горы.
Эту задачу предложил Иоганн Бернулли. Он объявил, что обладает замечательным решением своей задачи, но не хочет публиковать этого решения. Пускай крупнейшие математики попробуют показать свое искусство в решении этого нового типа математических задач. Иоганн Бернулли особо вызывал на состязание своего старшего брата Якоба, с которым он тогда резко враждовал и которого именовал невеждой 1.
Кривая, по которой санки спустятся в течение самого короткого времени, получила название «брахистохроны», от греческих слов брахос — короткий и хронос — время.
Задача о брахистохроне увлекла многих современников Бернулли. В задачах на максимум и минимум, которые исследовались до того времени, требовалось найти только одну особую точку на заданного вида кривой, в задаче же о брахистохроне надо было найти всю кривую, обладающую некими особыми свойствами — «наилучшими» ли, «наихудшими» ли, во всяком случае экстремальными свойствами.

Рис. 7-24. Пособие для демонстрации циклоиды.
По закраине доски катится круглый обруч. В обруче отверстие, куда вставлен грифель. Когда обруч катится, грифель описывает циклоиду.
Задача о брохистохроне положила начало новой ветви математики — вариационному исчислению. Это более тонкий и сложный инструмент для поисков лучших решений, нежели (Простое исследование на максимум и минимум.
Наиболее известное из первых решений задачи о брахистохроне дал «невежественный» Якоб Бернулли. Оказалось, что брахистохроной является незадолго до того открытая циклоида (рис. 7-24), т. е. кривая, которую описывает точка на окружности, когда эта окружность катится без скольжения по прямой линии. Циклоиду незадолго до того исследовал Гюйгенс и нашел, что если по этой кривой будет колебаться груз маятника, то период его колебания не будет зависеть от размаха. Поэтому циклоида называлась таутохронной кривой, т. е. кривой постоянного времени. Теперь оказалось, что она же является и брахистохроной.
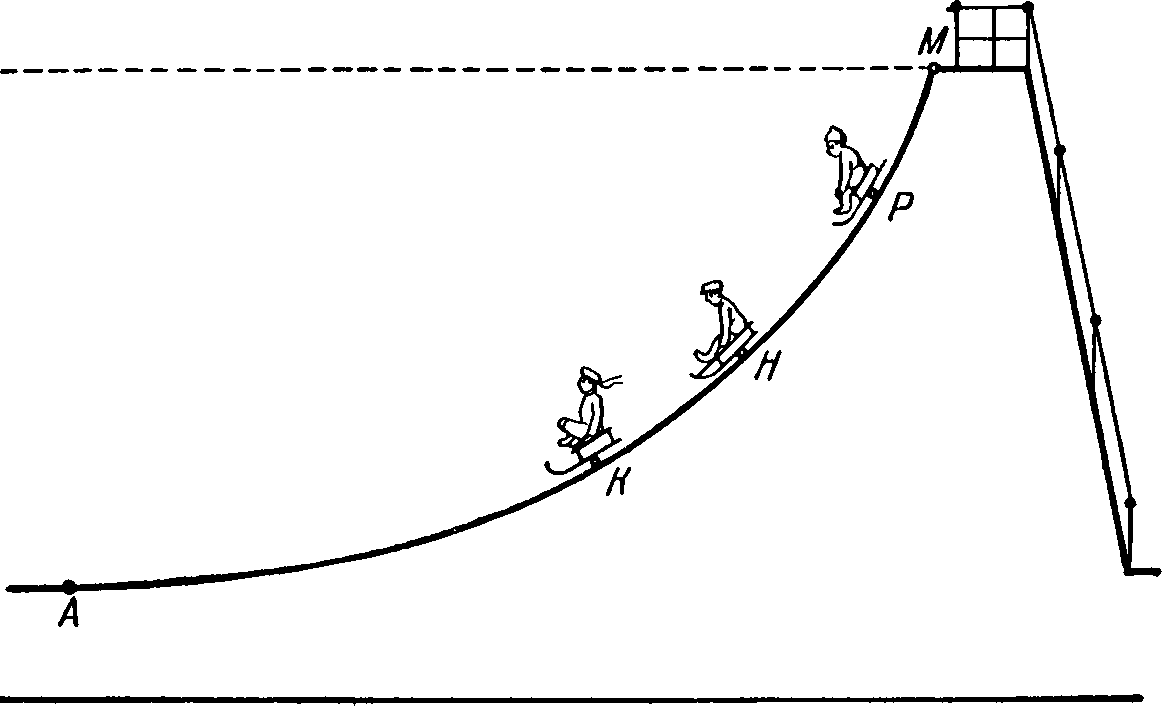
Рис. 7-25. Таутохронная гора.
Профиль горы имеет форму циклоиды. На разной высоте — пунктах К, Η, Р стоят готовые к старту салазки. Одновременно по команде салазки начинают скользить. Все трое достигнут основания горы — точки А одновременно. Здесь произойдет столкновение.
Санки скатываются с вершины горы в кратчайшее время, если вершину и подножье горы соединяет отрезок циклоиды. А если вершина горы и ее подножье к тому же так расположены, что между ними укладывается точно половина циклоиды, то на спуск как с вершины горы, так и с любого ее другого места вниз к подножью будет всегда затрачиваться одно и то же время (рис. 7-25).
7-26. Задача Дидоны
Изучение брахистохроны положило начало быстрому развитию вариационного исчисления, которое дало возможность находить различные кривые, удовлетворяющие требованию быть «самыми лучшими» для определенных условий. Но некоторые из задач о наилучших кривых были известны задолго до братьев Бернулли.
С древних времен дошла легенда о царице Дидоне, которая купила у финикийского царя Иорбаса столько земли, сколько может покрыть воловья шкура. Поведение Дидоны при покупке приводилось как пример хитрости. Она разрезала шкуру на тонкие ремешки, связала их все вместе и обвела ими большой участок земли.
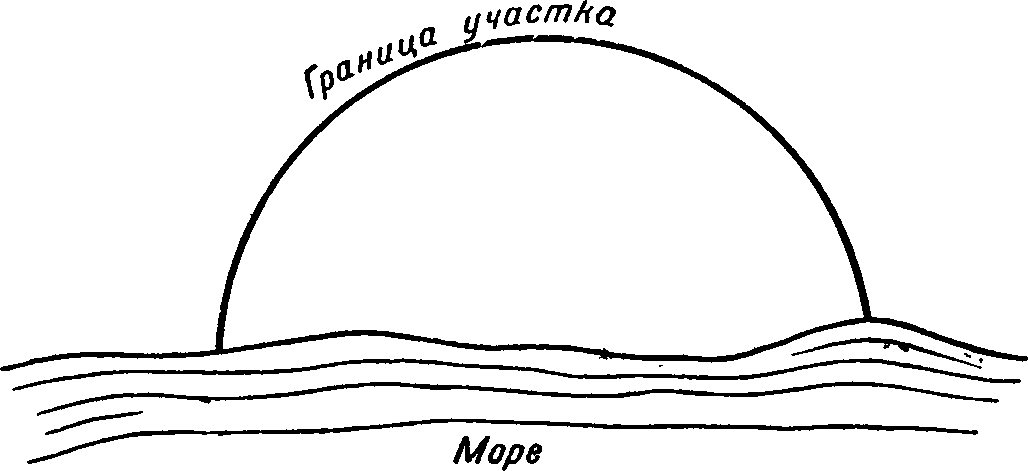
Рис. 7-26. Участок земли, имеющий наибольшую ценность при заданной длине сухопутной границы.
Концы ремешков Дидона не замкнула, а оставила на берегу моря, чтобы и на море распространить свою власть.
Эта легенда служит основой для серии математических задач: какая кривая при заданной длине охватывает наибольшую площадь? И с древних же времен было известно (интуитивно, без строгих доказательств, которые были даны много позже), что из всех геометрических фигур с заданным периметром наибольшую площадь имеет круг. А если кривая не замкнута, а опирается на какие-то точки, то между этими точками должны быть проведены дуги круга (рис. 7-26).
Задача Дидоны может быть усложнена допущением, что цена земли не всюду одинакова: чем ближе к берегу, тем дороже земля, а чем дальше от берега, тем стоимость земли меньше. И ремешком требуется охватить не наибольшую площадь, а наибольшей стоимости площадь. В зависимости от закона изменения стоимости получится та или иная кривая.
Вариационным методом можно исследовать и задачу о самой большом ящике из заданного листа жести.

Рис. 7-27. Приемный контур (виток), получающий наибольшую мощность (при заданном периметре 1) при расположении его вблизи прямолинейного проводника.
Когда периметр витка меньше, нежели расстояние от центра витка до токонесущего проводника, то наивыгоднейшая форма витка близка к окружности.
Чем меньше расстояние от провода до приемного витка, тем более приплюснутую и вытянутую форму должен иметь виток, чтобы захватить наибольший магнитный поток. Плотность магнитного потока пропорциональна 1/х.
В § 7-1 и 7-13 мы ограничивали себя условием, что по углам листа жести вырезаются прямолинейные четырехугольники. Но больший объем ящика получится, если вырезать из листа криволинейные фигуры. Очертания этих кривых надо отыскивать приемами вариационного исчисления.
7-27. Вариационные задачи в электротехнике
Задача Дидоны о кривой, охватывающей наибольшую площадь, может быть полезна при расчете некоторых случаев передачи энергии электромагнитной индукцией. В электротехнической версии эту задачу можно сформулировать так: требуется построить приемный виток, который охватывал бы наибольший магнитный поток. Заданными считаются длина проводника, из которого виток выполняется (периметр витка), и структура электромагнитного поля, в котором этот виток располагается.
Когда магнитное поле таково, что в пределах площади, охватываемой витком, сила поля меняется незначительно, то наибольший магнитный поток будет охвачен витком в форме круга. Но если магнитное поле неоднородно — в одних местах сильнее, a в других слабее, — то наилучший виток будет иметь очертания сложной кривой.
На рис. 7-27 показаны «наилучшие витки» вблизи прямолинейного, весьма протяженного проводника с током. В пространстве вокруг такого проводника магнитное поле изменяется по гиперболическому закону ![]() — магнитная напряженность обратно пропорциональна расстоянию от проводника.
— магнитная напряженность обратно пропорциональна расстоянию от проводника.
Другой пример применения вариационного метода — это вопрос о выборе наилучшей формы изолятора. В главе второй было сказано о том, что по всякому изолятору всегда происходит утечка тока. Эту утечку можно разделить на две составляющие: поверхностную и объемную. Ток объемной утечки идет через всю толщу изолятора. Поверхностная же утечка определяется очертанием поверхности изолятора. Большинство изоляторов — это тела вращения, и в них поверхностная утечка определяется формой образующей (профилем).
Важно подобрать такую форму поверхности изолятора, чтобы электрическое сопротивление поверхности было наибольшим и, следовательно, ток утечки по поверхности был бы наименьшим.
Бесчисленное количество кривых может быть использовано в качестве образующей поверхности изолятора. Вариационный анализ показывает, что сферическая поверхность изолятора имеет наименьшее поверхностное сопротивление, наибольшую поверхностную утечку. Всякая другая поверхность, отличная от сферической, будет иметь меньший ток утечки. Но наилучшей поверхности не существует.
В этой задаче вариационнокивысокихчастоый анализ не дает наилучшего, но указывает на наихудшее, на то, чего конструктору следует избегать.


