7-17. Высокочастотники и низкочастотники
В силовых сетях, идущих от центральных электростанций, циркулирует ток с частотой 50 Гц. Но для энергетических целей применяются также токи, имеющие частоту, в тысячи и миллионы раз более высокую. При всех частотах требуется передавать энергию с возможно более высоким к. п. д., но в разных областях это достигается разными приемами.
Низкочастотники — это те, кто работает с малыми запасами энергии на складах. За полупериод переменного тока в системе потребляется больше энергии, нежели ее может быть запасено и в электрических, и в магнитных полях.
У высокочастотников же наоборот — потребление энергии за полупериод переменного тока бывает значительно меньше запасов колебательной энергии в системе.
Хотя перед энергетиками — и высокочастотниками, и низкочастотниками — стоит одна и та же задача: минимальные потери при передаче электроэнергии, но конструктивные решения у них совершенно разные.
В трансформаторах со стальным сердечником на частоту тока 50 Гц выбирают малый ток холостого хода. Низкочастотники допускают в своих трансформаторах ток холостого хода — ток намагничивания, равный только одной десятой от рабочего тока, тока нагрузки.
В высокочастотных же трансформаторах без стального сердечника ток холостого хода может в несколько раз превышать нагрузочный.
Низкочастотники работают с большой связью между катушками своих трансформаторов. Коэффициент связи трансформаторов на 50 Гц обычно больше 0,9 — он близок к единице. Поэтому можно допускать большое затухание тока в катушках.
Высокочастотники строят трансформаторы, у которых связь между обмотками бывает значительно меньше единицы. Но зато они применяют обмотки с малым затуханием и этим обеспечивают такое же высокое или даже большее значение к. п. д., что и при низких частотах.
У высокочастотного трансформатора, показанного на рис. 7-14, коэффициент связи равен 0,6—0,8, но часто применяются и иные высокочастотные трансформаторы, у которых коэффициент связи лишь несколько сотых. Примером подобной конструкции является высокочастотный транспорт: между участком бесконтактной сети и приемным контуром на экипаже коэффициент связи бывает меньше 0,1.
И в пределах все той же «высокой частоты» применяются разные решения. При частотах до 50 кГц потери в катушках зависят главным образом от сечения меди в ее проводниках. Увеличивая вес меди, можно снижать потери. При более высоких частотах потери в значительной мере определяются изоляцией между витками.
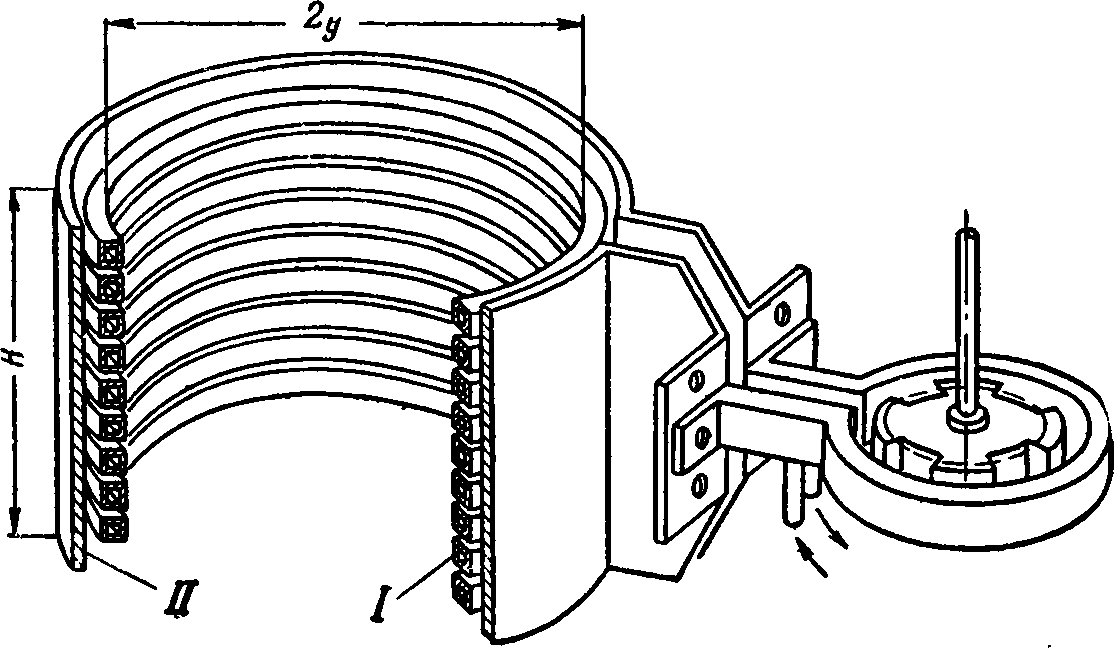
Рис. 7-14. Трансформатор без стального сердечника для установки высокочастотного нагрева.
I — первичная обмотка трансформатора из девяти витков медной трубки, охлаждаемой водой; II — вторичная обмотка из одного витка листовой меди.
К трансформатору подключен одновитковый нагревательный индуктор, внутри которого находится стальное изделие, нагреваемое под поверхностную закалку. Подобные воздушные трансформаторы применяются для токов с частотой от нескольких десятков до сотен тысяч герц.
Анализ на максимум и минимум показывает, что для разных условий работы существуют свои оптимальные числа витков обмотки, своя оптимальная высота трансформатора Н и его оптимальный диаметр 2у.
Увеличение расхода меди на трансформатор не повышает его к. п. д.
В каждой области частот свои допущения, свои упрощения. Низкочастотники считают, что сопротивление проводника определяется его сечением, они имеют дело с конструкциями, в которых ток равномерно распределен по всему сечению проводника. А высокочастотники принимают, что сопротивление проводника зависит от его периметра, высокочастотные токи проходят лишь в тонком поверхностном слое металла.
При низких частотах стальной сердечник улучшает передачу энергии между катушками. Вытащишь сердечник — трансформатор сгорит. А при высоких частотах,
наоборот, стальной сердечник вызывает увеличение потерь. Введешь в трансформатор сердечник — и он начнет перегреваться. А без сердечника трансформатор работает нормально.
В каждой области частот по-своему составляют уравнения для поисков оптимума, и оптимумы эти получаются совсем разные.
7-18. Частные максимумы и максимум максиморум
На рис. 7-15 показано питание нагрузки через Т-образную схему, в которой каждое плечо состоит из емкости и индуктивности. Каждое плечо представляет для переменного тока некоторое реактивное сопротивление х.
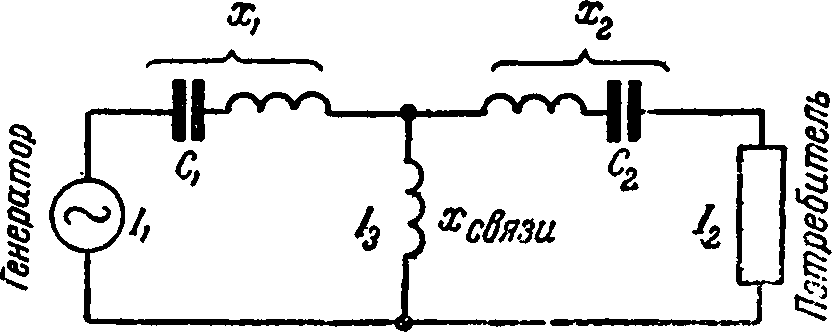
Рис. 7-15. Схема передачи энергии через цепь с большой реактивной мощностью.
Если напряжение генератора и сопротивление нагрузки неизменны, то ток через нагрузку можно менять, изменяя величину сопротивлений х1 и х2. Например, индуктивности плеч могут быть постоянными, а конденсаторы С1 и С2 переменными.
Изменение емкостей этих конденсаторов иногда называют настройкой схемы. Оставим одно из плеч, скажем, х1, неизменным, а реактивное сопротивление второго плеча будем менять. При некотором значении х2 ток через нагрузку — наибольший. Это называется резонансом. Но если теперь задать первому плечу новое значение х1' и, оставив его неизменным, вновь менять второе плечо, то наибольший ток получится при каком-то новом значении х2'. И величина этого тока будет иная, чем в первом случае.
Так можно задать первому плечу ряд значении и для каждого такого значения снимать зависимость тока нагрузки от сопротивления второго плеча. Получится ряд резонансных кривых.
Можно снимать резонансные кривые и по-иному — оставлять неизменным второе плечо х2, а менять величину первого плеча.
Таким образом получится множество «наибольших токов». Один из них будет самый больший, он соответствует какому-то определенному сочетанию х1и х2. Это значение тока максимальное из максимальных, его так и называют: максимум максиморум. Настройка на это значение тока называется полным резонансом. Все остальные максимумы тока — это частные максимумы, и настройка на них — это частный резонанс.
Отыскивая наиболее прочный кабель, мы меняли только одну величину — диаметр внутренней жилы кабеля. Это была система с одной степенью свободы. Она описывалась уравнением с одной независимой переменной.
В схеме рис. 7-15 два независимых переменных х1 и х2. Это схема с двумя степенями свободы.
7-19. Горная страна
Когда какая-либо величина зависит от двух переменных, то эту зависимость можно представить в виде некоторой поверхности. Так и зависимость тока нагрузки от двух сопротивлений плеч Т-образной схемы можно представить в виде модели какой-то сложной поверхности (из дерева, глины).
Чтобы изобразить эту сложную криволинейную поверхность на чертеже, часто прибегают к способу, принятому в топографии. Точки одинаковой высоты соединяют линиями, называемыми горизонталями. Горизонтали проводятся через определенные интервалы высоты. Если затем все горизонтали снести на одну плоскость, то получится система кривых. На каждой помечена соответствующая ей высота. В средней школе мы приучаемся представлять рельеф местности по подобным чертежам.
Густота горизонталей выражает крутизну скатов. Ямы и вершины окружены замкнутыми горизонталями.
Ложбины и мысовидные выступы характеризуются впадинами и выступами на горизонталях. Меж отдельных вершин находятся седловины. Здесь сходится несколько замкнутых горизонталей активного сопротивления первичного и вторичного контуров в схеме рис. 7-15..
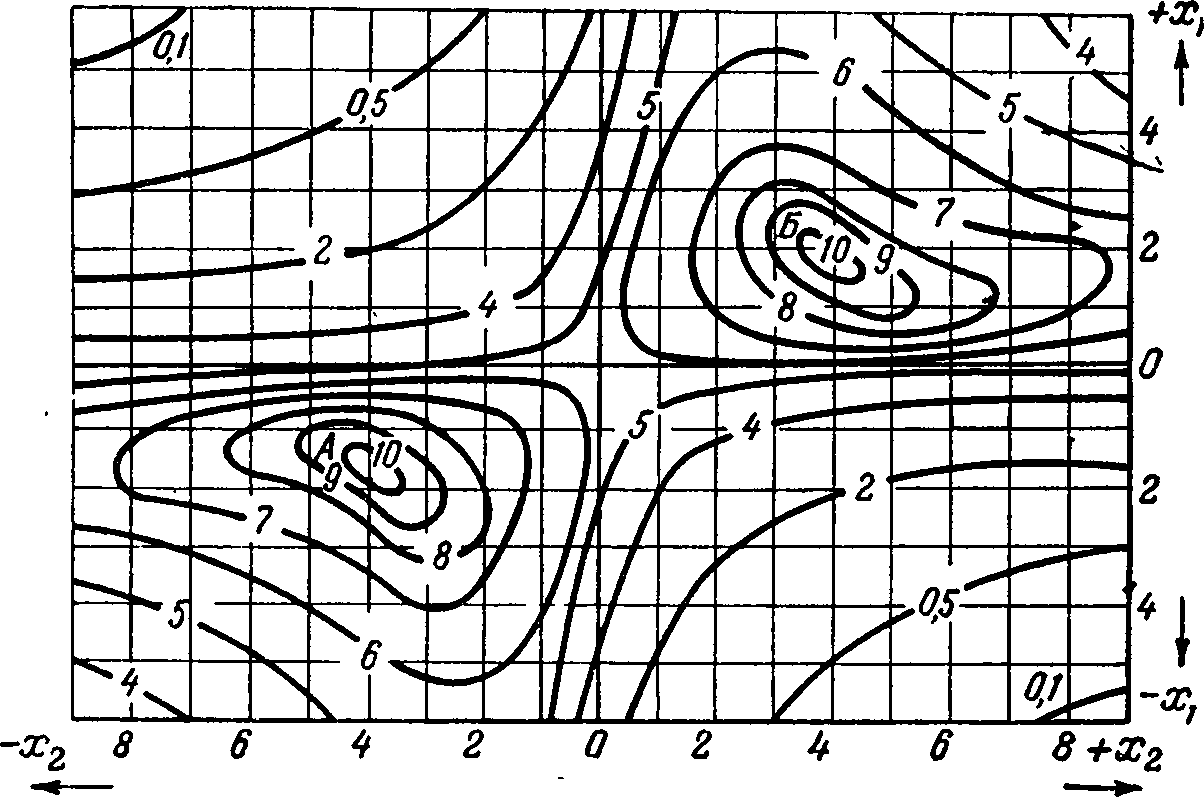
Рис. 7-16. Зависимость силы тока через нагрузку от реактивных сопротивлений первичного и вторичного контуров.
Горизонтальная линия, проведенная через середину чертежа — ось, на которой отложены значения реактивного сопротивления вторичного контура х2. Вправо от точки О эти значения положительны, влево — отрицательны. Вертикальная линия через середину чертежа — ось для реактивного сопротивления первичного контура х1.
Каждой комбинации сопротивлений х1 и х2 соответствует свое значение силы тока. На чертеже точки равной силы тока соединены линиями. На каждой такой кривой линии поставлена цифра, показывающая силу тока в относительных единицах.
На двух вершинах А и Б сила тока через нагрузку наибольшая (10 единиц). Любое изменение первичного или вторичного индуктивного сопротивления х1 или х2 вблизи этих вершин вызывает ослабление тока.
Взят численный пример, когда сопротивление генератора принято за единицу, сопротивление нагрузки в два раза больше, а сопротивление связи равно трем.
В представленной на рис. 7-16 местности может пролегать множество маршрутов. Если стать в точке х1=0 и х2=0, то любое движение по оси х1 или х2 даст уменьшение тока, однако если двигаться наискось, в особенности в направлении к вершинам А или Б, то ток через нагрузку увеличивается. При подобном маршруте х1 и х2 меняются одновременно. Так может быть, например, когда все емкости и индуктивности в схеме остаются неизменными, а меняется частота питающего генератора.
Задав, например, х1 какое-нибудь постоянное значение и изменяя х2, мы пересечем местность, оставаясь все время на одной «широте». При некотором значении х2 достигнем более высокой точки. По обе стороны от нее будет спуск. Это и будет частный резонанс.
Поочередно настраиваясь на частные резонансы, можно приблизиться, постепенно меняя то х1, то х2, к вершине А или вершине Б.
Рельеф местности зависит от соотношения активных и реактивных сопротивлений в схеме. Чем больше сопротивление связи по сравнению со средним геометрическим активных сопротивлений первичного и вторичного контуров, тем дальше раздвигаются вершины, соответствующие «максимумам максиморум», и тем круче скаты вершин. В нашем примере![]() . При уменьшении же разности
. При уменьшении же разности![]() обе вершины сближаются и при
обе вершины сближаются и при![]() они сливаются в одну, расположенную в центре. Это критическая связь.
они сливаются в одну, расположенную в центре. Это критическая связь.
На рис. 7-17 показаны три модели (каждая снята для наглядности в двух видах) для тока через нагрузку при разных соотношениях в схеме. На этих моделях в качестве «широты» и «долготы» взяты не значения реактивных сопротивлений плеч, а отношение собственных длин волн первичного и вторичного контуров к длине волны, вырабатываемой питающим генератором. Это отношение обратно отношению частот:![]()
Через эти модели можно провести секущие плоскости, перпендикулярные основанию. На этих сечениях получатся разнообразные резонансные кривые. Если, например, все сопротивления емкости и индуктивности схемы остаются неизменными, а меняется частота подводимого тока, то секущую плоскость надо провести через точку, соответствующую λ1 и λ2 и через начало координат (точку 0,0).
Рис. 7-17. Пространственные модели тока нагрузки в электрической цепи с двумя степенями свободы.
Вверху (а и b) — критическая связь
Посредине (с и d) — связь больше, чем критическая Оба контура — первичный и вторичный — имеют одинаковое затухание.
Внизу (е и f) — связь больше критической. Затухание первичного контура больше, нежели вторичного.

При сильной связи получаются двугорбые резонансные кривые. При критической и слабой связи получается одногорбая резонансная кривая, подобная кривой одиночного колебательного контура (рис. 7-18).
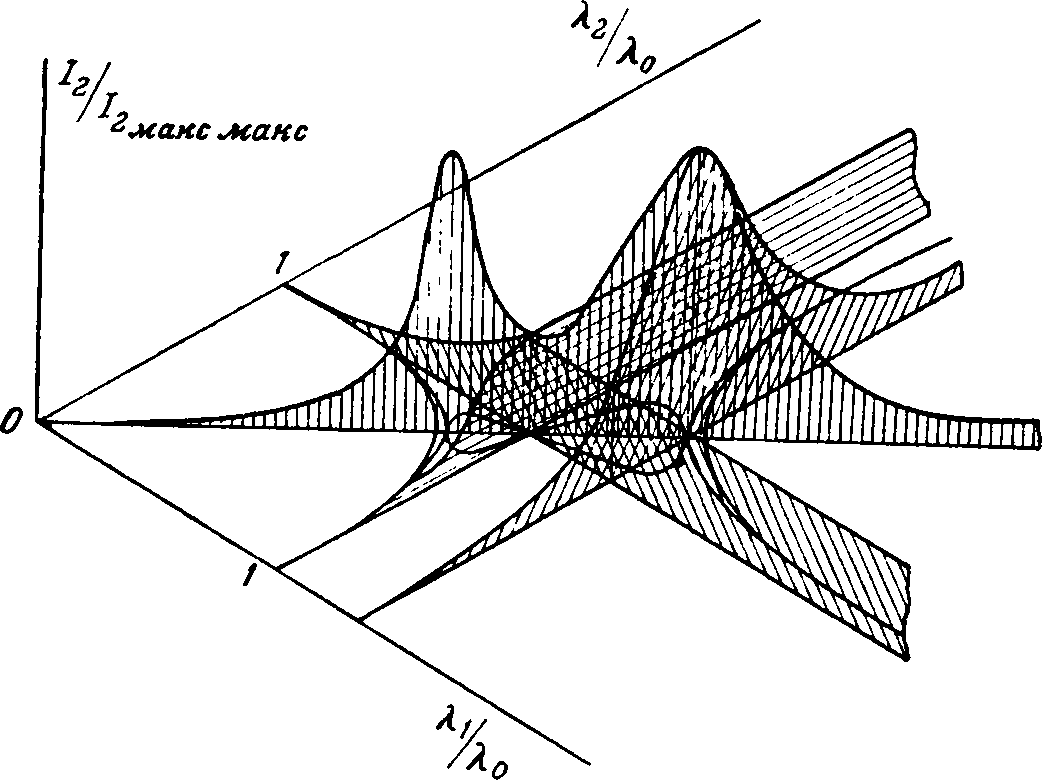
Рис. 7-18. Сечения пространственной модели тока вторичного контура.
Первичный и вторичный контуры имеют одинаковое затухание. Связь выше критической.
В зависимости от направления плоскости сечения получаются кривые разного профиля.
Две вершины наибольших максимумов тока лежат над биссектрисой угла плоскости![]() Сечение, проведенное через эту биссектрису,
Сечение, проведенное через эту биссектрису,
дает очертание двугорбой кривой. Другие плоскости сечения дают одногорбые кривые или кривые с горизонтальной частью большой протяженности — плоскогорья.
В схеме рис. 7-15 две степени свободы. Часто приходится сочетать большее число звеньев. Фильтр может представлять собой систему с тремя, четырьмя и более степенями свободы.
Чтобы геометрически представить систему с тремя независимыми переменными, с тремя степенями свободы, необходимо уже четырехмерное пространство. Или же для одной системы надо строить целый ряд трехмерных моделей. Огромные трудности стоят на пути анализа систем со многими степенями свободы.
Но во всех случаях самое трудное — это не анализ уже сформулированной зависимости. Труднее всего ставить вопросы, ибо это значит удить рыбу в океане; легче давать ответы. В правильно поставленном вопросе уже таится ответ.
Когда инженер приступает к поискам лучшего, самый ответственный момент — это составление уравнений. Если он правильно определил, в каком краю, в какой стране, в какой ее области производить поиски, то дальше построить точные карты всех вершин и ущелий дело только времени и терпения.


