Электричество работает - Рычаги

12-15. «Кости великана и морских животных»

«Сальвиати: ...Мы ясно видим невозможность не только для искусства, но и для самой природы беспредельно увеличивать размеры своих творений. Так, невозможна постройка судов, дворцов и храмов огромнейшей величины, коих весла, мачты, балки, железные скрепы, словом, все части держались бы прочно. С другой стороны, и природа не может произвести деревьев несоразмерной величины, так как ветви их, отягощенные собственным чрезвычайным весом, в конце концов сломались бы. Равным образом невозможно представить себе костяка человека, лошади или другого живого существа слишком большой величины, который бы держался и соответствовал своему назначению; достигнуть чрезвычайной величины животные могли бы только в том случае, если бы вещество их костей было значительно прочнее и крепче, нежели обычное, или же если бы кости их изменились, соразмерно увеличившись в толщину, отчего животные по строению и виду производили бы впечатление чрезвычайной толщины. Это уже было подмечено проницательным поэтом (Ариостом в «Неистовом Роланде»), который, описывая великана, говорит:
Нельзя было сказать, насколь он был высок, Так все в нем было непомерно толсто.
В качестве примера, только что сказанного, я покажу вам рисунок кости, удлиненной только в три раза, но увеличенной в толщину в такой мере, чтобы она могла служить для большого животного с той же надежностью, как меньшая кость служит для животного малого размера. Вы видите, какой несообразно толстой выглядит такая увеличенная кость. Отсюда ясно, что тот, кто, желая бы сохранить в огромном великане пропорцию членов обыкновенного человеческого тела, должен был бы найти для построения костей какое-либо иное, более удобное и прочное вещество или же должен был бы примириться с тем, чтобы большее тело человека обладало крепостью, сравнительно меньшею, чем тело человека обычной величины; увеличение размеров до чрезмерной величины имело бы следствием то, что тело было бы раздавлено и сломано тяжестью своего собственного веса. Обычно мы видим, что, уменьшая размеры тел, мы не уменьшаем в такой пропорции их прочности; в телах меньших замечается даже относительное увеличение ее. Так, я думаю, что небольшая собака может нести на себе двух или даже трех таких собак, в то время как лошадь едва ли может нести на спине одну только другую лошадь, равную ей по величине.
Симпличио. У меня есть достаточный повод сомневаться в справедливости сказанного вами, а именно —  огромная величина тела, встречаемая у рыб; так, например, кит¹ равен по величине, если я не ошибаюсь, десяти слонам, и, однако, тело его все же держится.
Сальвиати. Ваше сомнение, синьор Симпличио, заставляет меня припомнить еще одно, упущенное мной сначала из вида условие, при котором великаны и прочие огромные существа могут жить и двигаться не хуже малых животных. Вместо того, чтобы увеличивать толщину и прочность костей и других частей, предназначенных для поддержания собственного веса и веса прилегающих частей тела, можно, оставив строение и пропорцию костей прежними, уменьшать в значительной мере вес материи как самих костей, так и частей тела, к ним прилегающих и ими поддерживаемых. По этому пути и пошла природа в творении рыб, сделав кости и части тела не только легкими, но и вовсе лишенными веса.
Симпличио. Хорошо вижу, к чему клонится ваша речь, синьор Сальвиати. Вы хотите сказать, что так как местопребыванием рыб является вода, которая в силу своей тяжести отнимает вес у погруженных в нее тел, то материя, из коей состоят рыбы, теряя в воде вес, может держаться, не обременяя костей. Однако этого для меня недостаточно, ибо хотя и можно предположить, что кости рыб не отягощаются телом, но материя этих костей, конечно, имеет вес. Кто же может утверждать, что ребро кита, величиною с добрую балку, не имеет достаточно веса и не пойдет ко дну в воде? По вашей теории тела такого большого размера, как у кита, не должно было бы существовать.
Сальвиати. Чтобы лучше возразить на ваши доводы, я сначала предложу вам вопрос: видели ли вы когда-нибудь рыб в спокойной и неподвижной воде не опускавшимися ко дну, не поднимающимися на поверхность и не делающими никаких движений?

¹ В эпоху Галилея кита причисляли к рыбам.

Симпличио. Это всем известное явление.
Сальвиати. Но если рыбы могут пребывать в воде без всякого движения, то это является неоспоримым доказательством того, что вся совокупность объема их тела равна по удельному весу воде; а так как в их теле существуют части более тяжелые, нежели вода, то необходимо прийти к заключению, что есть и другие части, которые легче воды и создают равновесие. Так как кости являются более тяжелыми, то мясо или другие какие-либо органы должны быть легче воды, и они-то своей легкостью отнимают вес у костей. Таким образом, в воде имеет место совершенно обратное тому, что мы видим у наземных животных: в то время как у последних кости должны нести свой вес и вес мяса, у водяных животных мясо поддерживает не только свой вес, но и вес костей. Таким образом, нет ничего чудесного в том, что огромнейшие животные могут существовать в воде, но не на земле, т. е. в воздухе.

Сагредо. Мне очень понравились рассуждения синьора Симпличио, вопрос, им возбужденный, и разрешение последнего. Я заключаю из них, что если вытащить на берег одну из таких огромных рыб, то она не сможет долгое время держаться, так как связь между костями ее должна скоро порваться, и тело разрушится».
К этому можно добавить, что на планете, меньшей нежели Земля, — например, на астероиде, где мала сила тяжести, существо с размерами слона могло бы иметь тонкие и длинные ноги. А на большой планете — например, на Юпитере, где сила тяжести велика, и у существа размером с комара конечности должны были бы быть короткими и толстыми, а существо размерами со слона и вовсе невозможно.
Проведем теперь подобного рода рассуждения применительно к трансформаторам. Начнем с одного из простейших — с рычага.

12-16. Пределы применения рычагов

Мы уже говорили, что всякое перемещение одного конца рычага доходит до его другого конца только через некоторое время. Если колебать один конец рычага с большой частотой, то вдоль него побежит волна. Назовем скорость волны упругих колебаний в материале рычага ν. Это то расстояние, которое волна проходит за одну секунду. За период одного колебания Т волна распространится на расстояние νΤ, равное длине волны λ. Так как длительность периода колебаний обратно пропорциональна частоте T=l/f, то можно еще записать, что длина волны равна скорости, поделенной на частоту: h=v/f.
Размер плеча рычага определяется приложенной к нему силой F и допускаемой напряженностью в материале рычага. Обозначим эту механическую напряженность так же, как принято обозначать электрическую напряженность поля, — буквой Е. Чем больше сила и чем меньше допустимая напряженность, тем больше должны быть размеры рычага Z.
Примем:
Мощность, которая передается рычагом (обозначим ее через букву Р), равна произведению силы F на скорость движения рычага. Наибольшая, предельная скорость — это скорость упругих колебаний, которую мы обозначили через ν. Следовательно, наибольшая мощность, которую может передать рычаг, P = Fv. Но F, как мы только что сказали, пропорциональна Е1. Отсюда можно записать, что . Разделив обе части этой формулы на длину волны λ и заменив в правой части λ на v/f, окончательно получим:

Вот это и есть формула, которая дает связь между отношением Ζ/λ, т. е. типом конструкции механического трансформатора, и механическими характеристиками материала, из которого трансформатор построен, —  допустимой напряженностью в материале Е и скоростью распространения механических колебаний ν. Эта же формула показывает зависимость Ζ/λ от мощности и частоты колебаний.
Законы рычага «перемещение плеч прямо пропорционально длинам плеч» и «силы обратно пропорциональны длинам плеч» справедливы, только, когда размеры рычага l значительно меньше длины волны λ.
Это требованиеозначает, что и отношение не должно превышать некоторой определенной величины.
Таким образом, для каждого материала (каждого значения Е и ν) существуют предельные значения мощности Р и частоты f, которые можно передать при помощи рычага. При больших значениях произведения Pf отношение l/λ возрастает, трансформатор уже не может быть выполнен в виде рычага. Передача энергии уже будет определяться не теми примитивными законами рычага, которые приведены выше, а более сложными соотношениями распространения волновых процессов.
Увеличивая мощность Р надо уменьшать частоту f, если мы хотим обойтись рычагом. Для больших значений Pf рычаг осуществить невозможно.
Если же требуется одновременно и большая мощность, и высокая частота, то неизбежно применение не трансформатора-рычага, а трансформаторов волн типа рупоров, зеркал, линз — типа отражателей и преломителей.

12-17. Некоторые уточнения

В предыдущем параграфе мы произвольно приняли, что размер трансформатора l прямо пропорционален отношению силы к допустимой напряженности: Но в зависимости от типа конструкции трансформатора его размер может по-иному зависеть от F и Е; размеры l могут быть пропорциональны не первой степени, а корню (квадратному, кубическому) из отношения F/E.
В общем случае отношение l/λ будет пропорционально ; здесь показатели степени а, b, с и dмогут быть правильными дробями, но в некоторых случаях те или иные показатели могут быть и больше единицы.
В таком виде формула более универсальна и пригодна не только для механических, но и для всевозможных электромагнитных трансформаторов. Во всех случаях мощность и частота стоят в числителе, а допустимое напряжение и скорость распространения волнового процесса — в знаменателе.
При рассмотрении трансформаторов электромагнитной энергии мы вместо скорости механических колебаний υ подставляем в формулу скорость электромагнитной волны, которая равна скорости света в пустоте с, деленной наε — диэлектрическая проницаемость, μ — магнитная проницаемость материалов конструкции.
Ввиду большого разнообразия конструктивных форм трансформаторов электромагнитной энергии нельзя дать единой зависимости размеров конструкции от допустимых нагрузок материалов (плотностей тока в проводниках, магнитного потока в сердечниках — если они имеются — и электрического поля в изоляторах), а также от мощности и частоты.
У катушек со стальными сердечниками, если принять неизменную плотность тока в обмотках и неизменную плотность магнитного потока в сердечнике, мощность растет как четвертая степень линейных размеров: Р=l4¹.
У катушек без сердечников, если сохранять неизменную плотность тока в обмотках, мощность растет как пятая степень линейных размеров: Р=l5*.
В полых контурах колебательная мощность растет как объем, т. е. как куб линейных размеров.
Для зеркал мощность растет как квадрат линейных размеров.
Во всех случаях мы придем к заключению, что l/λ=Pafb, только показатели степеней будут разными при разных уточняющих предположениях. Обычно показатель степени а при Р меньше показателя bпри f; а может быть в пределах от 0,5 до 0,2. Таким образом, мы видим, что отношение l/λ растет с мощностью и частотой, но влияние частоты сильнее, чем влияние мощности.
Мы пришли к заключению, что при больших мощностях и высоких частотах отношение l/λ должно быть велико, но вовсе не обязательно обратное заключение, что при уменьшении мощности и частоты l/λ должно быть мало.
Выше мы говорили, что у слона ноги обязательно должны быть толстыми, но у маленького существа ноги не обязательно должны быть тонкими. Не может быть больших животных, у которых конечности во много раз длиннее своего поперечника, но существует сколько угодно маленьких животных, у которых лапы короткие, толстые, если это целесообразно при их образе жизни.
У кошки, например, конечности относительно короче, чем у жирафа; у соболя — относительно короче, чем у слона.
Трансформаторы с малой мощностью и частотой могут иметь большое отношение l/λ, если эго обусловлено их назначением.
Например, для радиоволн длиной в несколько десятков метров трансформаторы могут быть выполнены в виде катушек, размеры которых много меньше длины волны. Но если эти волны требуется излучить узким потоком, например, для направленной связи, то строят антенны, размеры которых превышают длину волны. И чем более остро направленный требуется луч, тем больше должно быть отношение l/λ антенны.
В установках для высокочастотного нагрева применяются иногда трансформаторы — полые контуры вместо катушечных потому, что это улучшает экранировку, уменьшает потери.
В маломощных измерительных устройствах часто применяют трансформаторы с большим отношением l/λ, так как при этом удается повысить точность измерений.
Остановимся теперь несколько подробнее на вопросе: когда катушечные трансформаторы надо снабжать сердечниками из ферромагнитного материала, а когда от этих ферромагнитных сердечников надо отказываться и замыкать переменный электромагнитный поток по воздуху?

12-18. Границы между стальным и воздушным царствами

Можно оценивать катушечный трансформатор (как, вообще говоря, и всякий другой) по различным показателям. Например, для заданной мощности или заданных потерь энергии сравнивать друг с другом различные типы трансформаторов по их объему, весу, стоимости. При рассмотрении каждого отдельного показателя можно найти свою пограничную точку, по одну сторону от которой надо применять стальные сердечники, а по другую отказываться от таковых.   
Совокупность всех возможных пограничных точек — это поверхность, проходящая в многомерном пространстве. Но не будем заниматься вопросом о границе во всем его многообразии; рассмотрим такой частный вопрос: как зависит мощность трансформатора от его размера — от количества меди, а также и стали, если применен сердечник. Нo и этот вопрос еще упростим: рассмотрим только одну из обмоток трансформатора, т. е. одну катушку.
Произведение индуктивности катушки L на круговую частоту переменного напряжения ω=2πf, приложенного к катушке, дает индуктивное сопротивление катушки х=Lω. Для трансформаторов это индуктивное сопротивление значительно больше активного сопротивления обмотки:.

Поэтому, умножив индуктивное сопротивление на квадрат тока через катушку, получим полную мощность катушки:.
Рассмотрим сначала катушки без стального сердечника. При заданных пропорциях катушки и неизменном числе витков в ней при увеличении ее размеров индуктивность растет пропорционально первой степени размера. Сечение обмотки растет как квадрат линейных размеров. Полный ток через обмотку равен произведению сечения обмотки на допустимую плотность тока. Квадрат полного тока пропорционален четвертой степени линейных размеров катушки, а мощность, следовательно, пятой степени линейных размеров и квадрату допустимой плотности тока:’.
Когда в катушке имеется стальной сердечник, то кажущаяся мощность катушки Sст будет определяться не только плотностью тока в обмотке, но и допустимой магнитной индукцией в сердечнике. Полный магнитный поток в стальном сердечнике равен произведению допустимой магнитной индукции В на площадь сердечника, т. е. магнитный поток пропорционален квадрату линейных размеров катушки. Полная мощность катушки с сердечником пропорциональна произведению магнитного потока в сердечнике на полный ток в обмотке. Но полный ток в обмотке, как уже выше было сказано, пропорционален сечению обмотки — квадрату линейных размеров катушки. Следовательно, мощность катушки со стальным сердечником растет как четвертая степень линейных размеров:

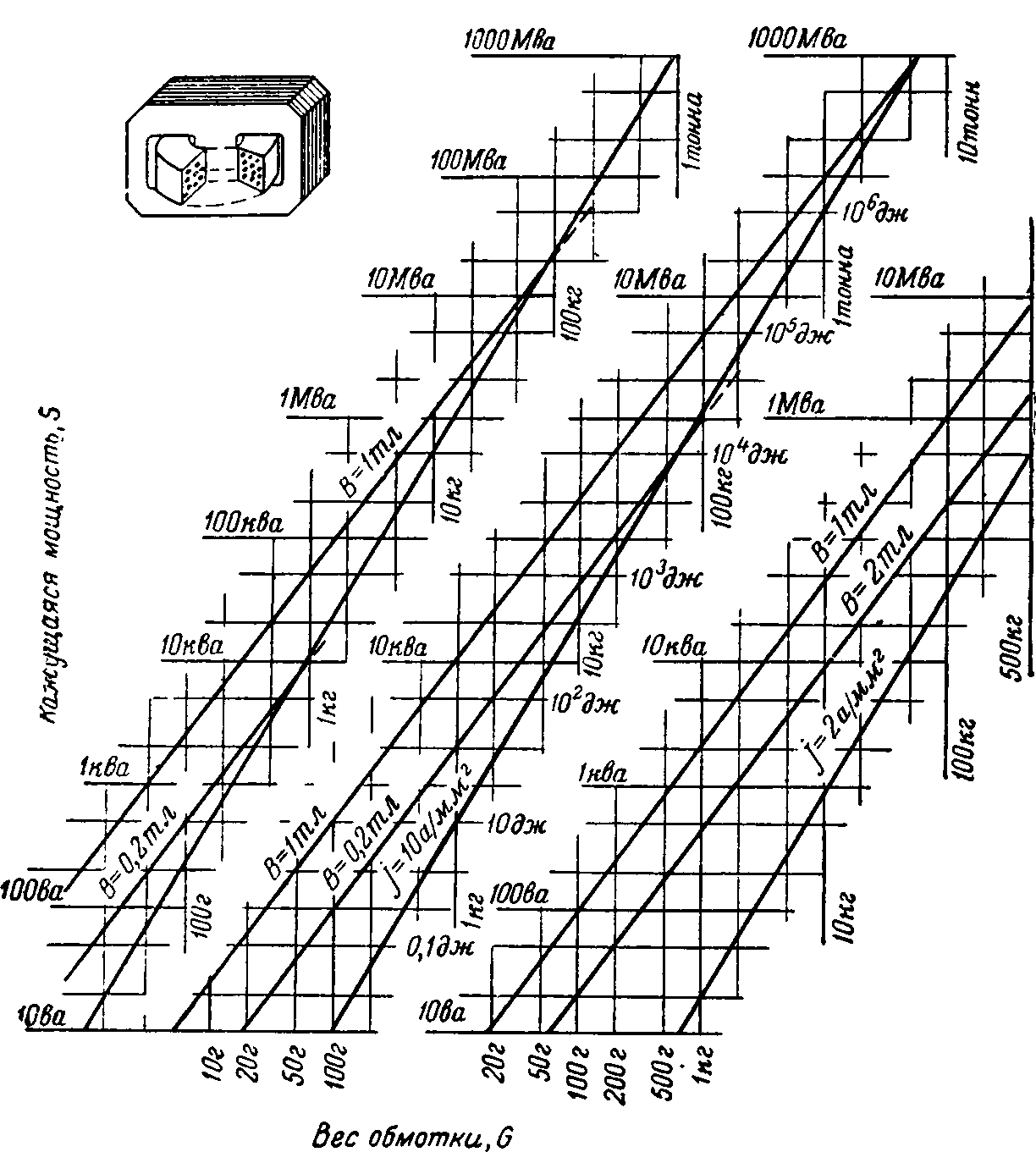
Рис. 12-7. К определению координат одного из пограничных пунктов между стальным и воздушным царствами. График зависимости мощности катушки от веса меди ее обмотки при разных допустимых нагрузках обмотки и сердечника.
По оси ординат отложена кажущаяся мощность катушки: S=Ul=LwI2. Частота тока входит в выражение для мощности как постоянный множитель, одинаковый для катушки с сердечником и бессердечниковой. График построен для частоты тока 50 Гц.
По оси абсцисс отложен вес медной обмотки. Чтобы лучше использовать площадь графика, по оси абсцисс даны три отдельных отрезка; на графике расположено три отдельных пучка, каждый из трех линий. В каждом пучке одна из трех линий идет более круто; эти круто идущие линии соответствуют катушкам без сердечника. Но две другие линии в каждом пучке пересекаются с «бессердечниковой линией» и соответствуют катушкам с сердечником при двух разных допустимых магнитных индукциях. Величина индукции в гауссах надписана над каждой линией. Для каждого пучка линий принята своя плотность тока в обмотке, одинаковая как в сердечниках, так и в бессердечниковых катушках.

Вес катушки (безразлично, с сердечником или без него) пропорционален кубу линейных размеров. Иначе  говоря, линейные размеры пропорциональны корню кубическому из веса катушки.
Если выразить вес катушки в граммах и обозначить его буквой G, а полную мощность Sв выразить в вольт- амперах, то для катушки из медного проводника без стального сердечника получим такое соотношение:

Плотность тока в этой формуле выражена в амперах на 1 мм², Необходимо указать также, что эта формула справедлива не для любой катушки, а для катушки оптимальных пропорций — такой, которая при заданной затрате проводникового материала имеет наибольшее отношение индуктивности к активному сопротивлению (подобные катушки иногда называются максвелловскими).
Для отношения реактивных мощностей катушки без сердечника и катушки, снабженной таковым, справедлива формула

Как и в предыдущих формулах, вес меди G указан в граммах, плотность тока в медной обмотке j — в амперах на 1 мм², а индукция в стальном сердечнике В — в гауссах.
Когда отношениеравно единице, то это пограничная точка. При больших соотношениях надо отказываться от стального сердечника, при меньших —  применять сердечник. Вес пограничной медной катушки определяется соотношением G=(0,2B/j)3.

В бессердечниковых катушках величина магнитной индукции не ограничена, и при неизменной плотности тока в обмотке магнитная индукция растет пропорционально линейным размерам катушки (пропорционально корню кубическому из веса катушки). В катушке же с сердечником принято, что магнитная индукция сохраняет одну и ту же величину независимо от размера и веса катушки.
При малой плотности тока в обмотке (крайний правый пучок линий соответствует j=2а/мм²) даже в очень больших катушках выгодно применять стальные сердечники. При большей плотности тока (крайний левый пучок j=50 а/мм²) магнитная индукция внутри бессердечниковой катушки уже при весе 100 кг превышает допустимую для стального сердечника величину 10 000 г, и, следовательно, при больших весах катушки удаление сердечника повышает мощность катушки.
Если допустимая индукция 104 гс, а плотность тока 2 а/мм², то от стального сердечника надо отказываться для катушек весом более 1 000 т. Но если при той же магнитной индукции плотность тока будет 200 А/мм² (такая высокая плотность может быть допущена при импульсных режимах работы с большой скважностью), то стальной сердечник становится невыгоден уже для катушек весом более 1 кг.
В вышеприведенных рассуждениях не отражено влияние частоты. Оно проявляется в том, что по мере повышения частоты приходится выбирать меньшую допустимую магнитную индукцию в стальном сердечнике. Определим числовую зависимость для реактивной мощности катушек без стального сердечника и с ним при частоте тока 50 Гц:

По этим формулам построен график (рис. 12-8). По оси ординат отложены реактивные мощности катушек, общие для всех кривых. По оси абсцисс даны три отдельные шкалы весов меди, каждая для своего пучка линий.
В левом пучке, построенном для плотности тока 50 а/мм², нижняя линия, соответствующая катушке без сердечника, пересекает линию, соответствующую катушке с сердечником, допускающим индукцию 104 га при весе меди, равном 64 кг. Это соответствует кажущейся мощности катушки около 15 000 ква.
При больших мощностях катушки без стального сердечника выгоднее катушек, у которых имеется такой сердечник. Поэтому токоограничивающие реакторы в энергосистемах обычно выполняются без стальных сердечников. В длительном режиме при нормальной работе плотность тока в обмотках этих реакторов не превышает 4 a/мм². Но в момент короткого замыкания (именно тогда и проявляется действие токоограничивающего реактора) плотность тока в обмотках может более чем в 10 раз превысить плотность тока длительного режима. Мощность токоограничивающего реактора в моменты короткого замыкания измеряется часто сотнями тысяч и даже миллионами киловольтампер. При таких данных введение стального сердечника увеличило бы размеры, вес и стоимость реактора.
Вышеприведенные формулы и график рис. 12-7 определяют лишь один пограничный пункт между воздушным и стальным царствами. При движении по иным путям приходится пересекать границу в других точках. На практике часто отказываются от стальных сердечников при значительно меньших весах, меньших мощностях катушек.
Можно анализировать конструкции катушек в зависимости от потерь в них, от их к. п. д. Потери в катушке определяются ее декрементом δ. Эта величина равна отношению активного сопротивления катушки Rк реактивному х. Активное сопротивление — сопротивление потерь катушки — состоит из нескольких слагающих. Главные из них — это два: 1) потери, вызванные омическим сопротивлением обмотки катушки, и 2) потери на перемагничивание стального сердечника.
Когда второе слагающее становится больше первого, от сердечника надо отказываться.
Выше уже было сказано, что индуктивность катушки пропорциональна ее линейным размерам. Омическое же сопротивление обратно пропорционально линейным размерам (сечение витка растет как квадрат линейных размеров, а длина витка — как линейный размер). Поэтому отношение индуктивности к активному сопротивлению катушки пропорционально квадрату линейных размеров (весу в степени 2/3). Для декремента катушки без сердечника можно вывести следующее соотношение

Подразумевается катушка, выполненная из медной проволоки, имеющая оптимальные пропорции (максвелловская катушка), подразумевается также, что ток равномерно распределен по сечению проводников —  плотность тока во всех точках обмотки одна и та же.
В стальном магнитопроводе, который может быть помещен в катушку, возникает два вида потерь: 1) потери на перемагничивание — на гистерезис и 2) потери на вихревые токи. Чем больше сумма этих потерь, тем меньше пользы от сердечника. При некотором отношении потерь в сердечнике к декременту катушки без сердечника от сердечника надо отказываться вовсе.
С некоторыми допущениями можно записать условие отказа от стального сердечника:. Это — данные другого пограничного пункта на пути из воздушного в стальное царство. На этом пути не отражена зависимость от j и В.
Непрестанно разрабатываются все новые и новые материалы для сердечников (магнитно-мягкие материалы), допускающие большую индукцию и обладающие малыми потерями. В последние годы появились керамические магнитные материалы — оксиферы, в которых потери на вихревые токи отсутствуют даже при очень высоких частотах. Эти магнитные глины отодвигают границу применения сердечников в область больших мощностей и частот. Но появляются и конструкции проводников, которые дают преимущество бессердечниковым катушкам. Все время идет борьба различных конструкций, различных инженерных идей на границе стали и воздуха.

12-19. Точность, искажения, к. п. д.²

В парках выставляют иногда для развлечения публики кривые зеркала — цилиндрические, конические, волнистые. Зрители видят себя · в них растянутыми, сплюснутыми, изогнутыми самым причудливым образом. А то, что принято называть хорошим зеркалом — какое оно дает изображение? Говорят, неискаженное. Так ли это? Попробуем вдеть нитку в иголку, глядя на их изображение в зеркале. Или попробуем — что, казалось бы, еще проще — читать книгу, отраженную в зеркале.
Изображение в плоском зеркале очень похоже на сам предмет, но вместе с тем и отлично от него. В зеркальном отражении то, что в оригинале было справа, оказалось слева.
Всякая трансформация — это искажение. Если нет искажения, то нет и трансформации. Но в разных случаях к вопросу об искажениях разный подход.

В начале этой главы упоминались щипцы для орехов как пример механического трансформатора. В щипцах орех можно положить и дальше и ближе к шарниру. Во время раздавливания орех может передвинуться с одного места на другое. Коэффициент трансформации щипцов — величина непостоянная. Но для их работы такое постоянство и не требуется.
Существуют механические трансформаторы иных типов. В чертежном деле, например, применяется так называемый пантограф. Это — система сочлененных рычагов с двумя штифтами. Одним штифтом обводят копируемый чертеж. Второй штифт воспроизводит чертеж в измененном виде — увеличенном или уменьшенном. Иногда по разным осям производится разное уменьшение или увеличение. От пантографа требуется высокая точность работы. В данном случае понятие «точность» подразумевает строгое постоянство коэффициента трансформации.
Для многих типов трансформаторов вопрос о точности несуществен. В рычажном домкрате, например, коэффициент трансформации меняется в несколько раз при изменении высоты подъема. Но это обстоятельство мало кого беспокоит. От многих типов трансформаторов требуется только обеспечить малые потери энергии при трансформации, высокий к. п. д. Для других типов трансформаторов значение к. п. д. совершенно несущественно, зато требуется высокая точность. Таков упомянутый пантограф.
От большинства оптических трансформаторов требуются и высокая точность, и малые потери. Вопрос о точности оптических трансформаторов очень сложен. Один только перечень типов искажений, возможных в оптических приборах, может занять много страниц, потребует разъяснения множества специальных терминов. Например, для съемки и проектирования широкоэкранных фильмов применяется специальная — анаморфотная, как ее называют, оптика. При съемке изображение сжимается в горизонтальном направлении. На пленке той же ширины, что и для обычных фильмов, удается уместить значительно большую часть пространства, находящегося перед съемочным аппаратом. При проектировании фильма другая анаморфотная насадка растягивает изображение в ширину на экран. Изображение на экране получается неискаженным (рис. 12-8).

¹ Эту зависимость докажем в последующих разделах.

² Законы четности здесь не обсуждаются.

Рис. 12-8. Вверху — изображение для широкого экрана, снятое на кинокадр обычных размеров. При такой съемке цилиндрические стекла (съемочная анаморфотная оптика) снимают световой поток по горизонтали. При проектировании с пленки на экран (рисунок внизу) другие цилиндрические стекла (проекционная анаморфотная оптика) растягивают по горизонтали световой поток во столько раз, во сколько он был сжат при съемке. В результате изображение на экране воспринимается как неискаженное.

 Есть некоторые типы искажений, которые встречаются в различных типах трансформаторах: и в оптических, и в электротехнических (катушечных и других). Это так называемые частотные искажения. Суть их в том, что для колебаний разных частот коэффициент трансформации имеет разное значение. Когда к трансформатору подводится смесь колебаний различных частот, то соотношение мощностей различных частот на выходе не соответствует соотношению на входе.
Для световых лучей разные частоты означают разные цвета. В оптических приборах частотные искажения называются цветными (хроматическими). Лучи разного цвета, т. е. разной частоты колебаний, разной длины волн, распространяются с разной скоростью в различных прозрачных средах. Поэтому стеклянные призмы по-разному отклоняют лучи разных частот. Так разлагают белый свет в спектр. Простая стеклянная линза дает на экране изображение, которое окружено радужным ободком. В сложных составных линзах, применяя различные сорта стекол, можно добиться того, что коэффициент трансформации одинаков почти для всех цветов. Такие оптические устройства называются ахроматическими — не имеющими хроматических искажений.
Частотные искажения встречаются и в различных акустических устройствах; например, громкоговоритель по-разному излучает колебания разных частот: более слабо — как очень низкие, так и очень высокие частоты, более сильно — некоторые средние частоты. Применяя электрические цепи, вносящие частотные искажения различного типа, можно в результате сильно ослабить частотные искажения при записи звука, его передаче и воспроизведении.