Производство электрических аппаратов управления и защиты - Точечные диаграммы и кривые рассеяния

Как уже отмечалось, из-за множественности факторов, влияющих на процесс изготовления одних и тех же деталей, на одном и том же оборудовании, при неизменном технологическом процессе, неизбежно имеет место рассеяние размеров и других заданных параметров изделий. Это явление получило название «рассеяние характеристик качества изделий» [8].
С целью анализа характера рассеяния по полученным отклонениям от номинального значения той или иной по количеству партии однородных деталей данные этих отклонений заносят в таблицу. По этим данным строят так называемые точечные диаграммы, совмещая последние с кривыми рассеяния. Характер подобных диаграмм приведен на рис. 2-10, где А — значение рассматриваемого параметра изделий; А1, А2,... AN — наблюдаемый ряд значений параметра; Анм и Анб — соответственно наименьшее и наибольшее значение параметра А; 1, 2, 3, ..., i — порядковый номер изделий в партии; ω — значение поля рассеяния; п1, п2, n3, ..., nΝ —количество деталей, имеющих Анм-, А2, ..., Αn- значение параметра. Каждой точке на диаграмме соответствует значение рассеяния параметра A определенного изделия, а количество точек равняется количеству деталей в партии. Значение поля рассеяния ω определяется зависимостью: ω = Αнб—Анм. По точечной диаграмме строят кривую рассеяния. Для этого по оси ординат откладывают ряд значений параметра А а по оси абсцисс — количество изделий, имеющих определенное значение параметра.
Характер кривых рассеяния размеров заготовок в большинстве случаев схож с только что рассмотренной и приведенной на рис. 2-10 диаграмме.
Количественный закон распределения рассеяния размеров рассматриваемой партии изготовленных деталей определяется кривой, огибающей крайние значения.

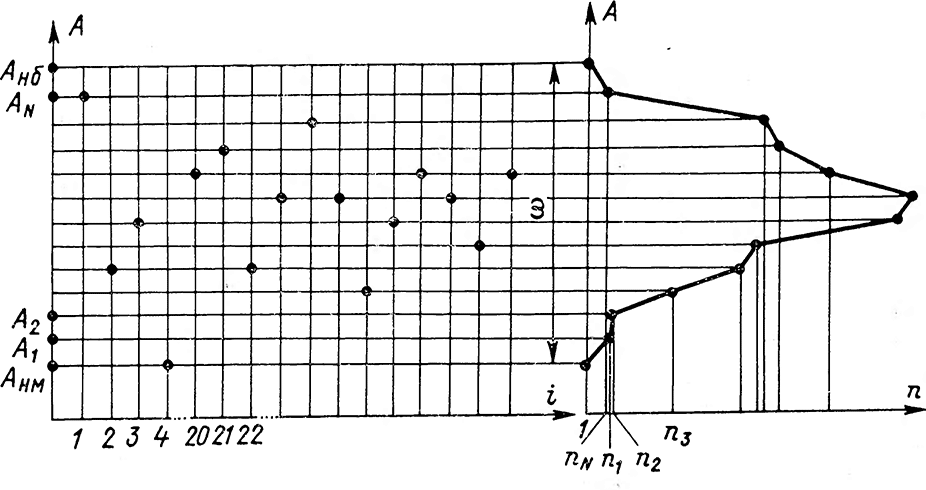
Рис. 2-10
Вероятность случайного явления. Теория вероятностей, являясь математической дисциплиной, изучает случайные явления, поддающиеся количественному анализу, т. е. те, которые подчиняются определенным закономерностям. В основе анализа случайных явлений лежит понятие вероятности. Если определенная величина случайных отклонений от номинального значения А наблюдается в среднем k раз среди п всех единичных наблюдаемых случаев, то вероятность Р отклонений А при данных неизменных условиях определяется отношением:

при этом все п случайных отклонений предполагаются равновозможными, единственно возможными, несовместными.
Равновозможными могут быть все случаи наблюдаемых отклонений размеров от номинальной величины, которые может принимать любая идентичная деталь в рассматриваемой партии.
Принцип единственно возможных случаев характеризуется тем, что наблюдаемый ряд размеров деталей А1, А2,..Ап, включая все случаи отклонений размеров от номинального, тем самым образует полную группу случаев п, и в партии деталей хотя бы одна из них будет соответствовать одному члену ряда.
Принцип несовместности означает, что у детали любой размер не может одновременно быть равен двум значениям.
Кроме того, различают еще невозможные и достоверные события (случаи). Вероятность невозможного события равна нулю; вероятность достоверного случая (k = n) равна единице.